Question

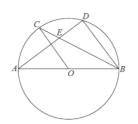
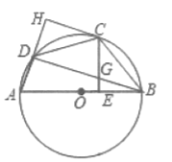
【题目】如图，四边形内接于为直径， ．

过点作于点交的延长线于点，连接交于点．

求证： 是的切线；

若点为的中点，求证：

若，求的长．

Answer 1

【答案】（1）见解析；（2）见解析；（3）16．

【解析】

（1）连接OC，OD，先证∠BAH=∠BOC，可得AH//OC，则OC⊥CH，即可证明；

（2）连接AC，先证CE=CH，再证Rt△CEB≌Rt△CHD（HL），则BE=DH，证出AD=DH，即可得到结论；

（3）延长CE交⊙O于点F.得出GB=GC=5。在Rt△GEB中，sin∠GBE=,易求

GE=3，再运用勾股定理求出BE，然后证得Rt△AEC∽Rt△CEB可得，易求

AE的长，再求出AD，最后求出BD的长即可．

CE-BE

证明：如图，连结

又

是的切线；

证明：如图，连接

又

又

点为的中点

，

；

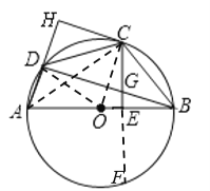
解：如图，延长交于点

是的直径，

在中，

即

在中，

．