题目内容
【题目】(一)问题提出：如何把n个边长为1的正方形，剪拼成一个大正方形？
(二)解决方法
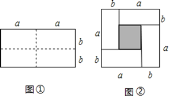
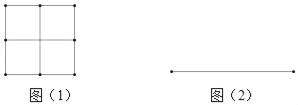
探究一：若n是完全平方数，我们不用剪切小正方形，可直接将小正方形拼成一个大正方形，如图(1)，用四个边长为1的小正方形可以拼成一个大正方形．
问题1：请用9个边长为1的小正方形在图(2)的位置拼成一个大正方形．
探究二：若n＝2，5，10，13等这些数，都可以用两个正整数的平方和来表示，以n＝5为例，用5个边长为1的小正方形剪拼成一个大正方形．
(1)计算：拼成的大正方形的面积为5，边长为
，可表示成
；
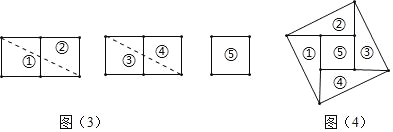
(2)剪切：如图(3)将5个小正方形按如图所示分成5部分，虚线为剪切线；
(3)拼图：以图(3)中的虚线为边，拼成一个边长为的大正方形，如图(4)．
问题2：请仿照上面的研究方式，用13个边长为1的小正方形剪拼成一个大正方形；
(1)计算：拼成的大正方形的面积为____，边长为_____，可表示成____；
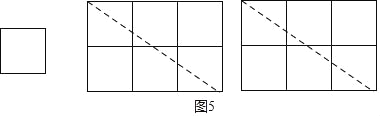
(2)剪切：请仿照图(3)的方法，在图(5)的位置画出图形．
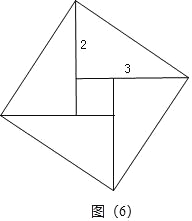
(3)拼图：请仿照图(4)的方法，在图(6)的位置出拼成的图．
【答案】探究一：所拼图形见解析；探究二：(1)13，
，＝
；(2)见解析；(3)见解析；
【解析】
探究一：由大正方形的面积计算出边长，从而可画出图形；
探究二：(1) 13个边长为1的正方形的面积为13，即可求出边长.
(2)将13正正方形分割为1个边长为1的正方形和4个两直角边分别为2和3的直角三角形即可；
(3) 仿照图(4)的方法，拼图即可.
解：探究一：∵9个边长为1的正方形的面积为9，
∴所拼成的正方形的边长为3．
所拼图形如图(2)所示：
探究二：(1)拼成的大正方形的面积为13，边长为，可表示成＝；
故答案为：13，，＝；
(2)如图(5)所示：
(3)拼成的图形如图(6)所示：
名校课堂系列答案
