Question

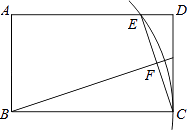
【题目】如图，扇形OMN与正方形ABCD，半径OM与边AB重合，弧MN的长等于AB的长，已知AB=2，扇形OMN沿着正方形ABCD逆时针滚动到点O首次与正方形的某顶点重合时停止，则点O经过的路径长 ．

Answer 1

【答案】2+4π
【解析】解：当扇形绕B旋转时，路径长是 =2π，

当弧NM在BC上时，O经过的路径长是2；

当扇形绕C旋转时，路径长是 =2π；

则点O经过的路径长2+2π+2π=2+4π．

故答案是：2+4π．

【考点精析】掌握弧长计算公式是解答本题的根本，需要知道若设⊙O半径为R，n°的圆心角所对的弧长为l，则l=nπr/180;注意：在应用弧长公式进行计算时，要注意公式中n的意义．n表示1°圆心角的倍数，它是不带单位的．