题目内容
【题目】如图,已知AD是△ABC的角平分线,⊙O经过A、B、D三点,过点B作BE∥AD,交⊙O于点E,连接ED.
(1)求证:ED∥AC;
(2)连接AE,试证明:ABCD=AEAC.
【答案】
(1)解:∵BE∥AD,
∴∠E=∠ADE,
∵∠BAD=∠E,
∴∠BAD=∠ADE,
∵AD是△ABC的角平分线,
∴∠BAD=∠CAD,
∴∠CAD=∠ADE,
∴ED∥AC;
(2)解:连接AE, 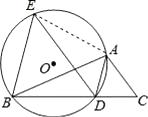
∵∠CAD=∠ADE,∠ADE=∠ABE,
∴∠CAD=∠ABE,
∵∠ADC+∠ADB=180°,∠ADB+∠AEB=180°,
∴∠ADC=∠AEB,
∴△ADC∽△BEA,
∴AC:AB=CD:AE,
∴ABCD=AEAC.
【解析】(1)根据平行线的性质得出∠E=∠ADE,又根据同弧所对的圆周角相等及等量代换得出∠BAD=∠ADE,根据角平分线的定义得出∠BAD=∠CAD,从而得出∠CAD=∠ADE,根据内错角星等二直线平行得出结论;
(2)连接AE,首先根据同弧所对的圆周角相等及等量代换得出∠CAD=∠ABE,然后根据同角的补角相等得出∠ADC=∠AEB,进而判断出△ADC∽△BEA,根据相似三角形对应边成比例得出结论。
【考点精析】本题主要考查了角的平分线和平行线的判定与性质的相关知识点,需要掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能正确解答此题.

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案【题目】某水果店计划进A,B两种水果共140千克,这两种水果的进价和售价如表所示
进价 | 售价 | |
A种水果 | 5 | 8 |
B种水果 | 9 | 13 |
![]() 若该水果店购进这两种水果共花费1020元,求该水果店分别购进A,B两种水果各多少千克?
若该水果店购进这两种水果共花费1020元,求该水果店分别购进A,B两种水果各多少千克?
![]() 在
在![]() 的基础上,为了迎接春节的来临,水果店老板决定把A种水果全部八折出售,B种水果全部降价
的基础上,为了迎接春节的来临,水果店老板决定把A种水果全部八折出售,B种水果全部降价![]() 出售,那么售完后共获利多少元?
出售,那么售完后共获利多少元?