题目内容
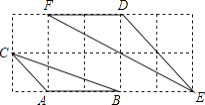
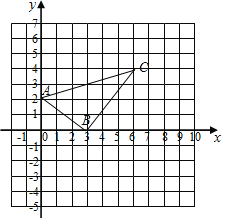
【题目】如图，在平面直角坐标系中，已知A（0，a），B（b，0），C（6，c）三点，其中a，b，c满足关系式|a-2|+（b-3）2+
=0，
（1）求A．B．C的坐标；
（2）求三角形ABC的面积；
（3）在y轴上是否存在点P，使三角形APC的面积与三角形ABC的面积相等？若存在，求出点P的坐标；若不存在，请说明理由．
【答案】（1）A（0，2）B（3，0）C（6，4）（2）6（3）（0，-2）或（0，4）
【解析】
（1）利用非负数的性质即可解决问题．
（2）利用分割法求三角形的面积即可．
（3）设P（0，m），构建方程即可解决问题．
解：（1）∵|a-2|+（b-3）2+
=0，
又∵|a-2|≥0，（b-3）2≥0，≥0，
∴a=2，b=3，c=4，
∴A（0，2）B（3，0）C（6，4）．
（2）S△ABC=4×6-
×2×3-×2×6-×6×3=6
（3）设P（0，m），
由题意：×|m-2|×6=6，
∴m=4或-2，
P（0，-2）或（0，4）
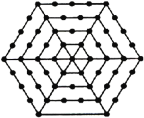
【题目】如图，有一个形如六边形的点阵，它的中心是一个点，作为第一层，第二层每边有两个点，第三层每边有三个点，依此类推．
（1）填写下表：
层 数 | 1 | 2 | 3 | 4 | 5 | … |
该层对应的点数 | 1 | 6 | … |
（2）写出第n层所对应的点数（n≥2）．
（3）如果某一层共96个点，你知道它是第几层吗？
（4）有没有一层，它的点数为100个？
（5）写出n层的六边形点阵的总点数．
【题目】某公司为一种新型电子产品在该城市的特约经销商，已知每件产品的进价为40元，该公司每年销售这种产品的其他开支（不含进货价）总计100万元，在销售过程中得知，年销售量y（万件）与销售单价x（元）之间存在如表所示的函数关系，并且发现y是x的一次函数．
销售单价x（元） | 50 | 60 | 70 | 80 |
销售数量y（万件） | 5.5 | 5 | 4.5 | 4 |
（1）求y与x的函数关系式；
（2）问：当销售单价x为何值时，该公司年利润最大？并求出这个最大值；
【备注：年利润=年销售额﹣总进货价﹣其他开支】
（3）若公司希望年利润不低于60万元，请你帮助该公司确定销售单价的范围．
