题目内容
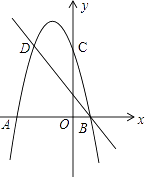
【题目】如图,AB是⊙O的直径,AE是弦,直线CG与⊙O相切于点C,CG∥AE,CG与BA的延长线交于点G,过点C作CD⊥AB于点D,交AE于点F. 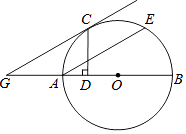
(1)求证: ![]() ;
;
(2)若∠EAB=30°,CF=a,写出求四边形GAFC周长的思路.
【答案】
(1)证明:连接OC,如图.
∵直线CG与⊙O相切于点C,
∴CG⊥OC.
∵CG∥AE,
∴AE⊥OC.
又∵OC为⊙O的半径,
∴ ![]()
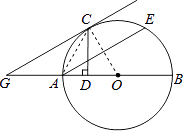
(2)证明:解:连接AC,如图.
由∠EAB=30°,CG∥AE,可得∠CGB=30°,
又由直线CG与⊙O相切于点C,∠AOC=60°,
可推出△AOC是等边三角形,
由△AOC是等边三角形,∠EAB=30°,CF=a,
可得∠CAF=∠ACF=30°,CF=AF=a,DF= ![]() ,
,
AD= ![]() ,
,
利用CG∥AE,可得到△ADF∽△GDC,从而推出AG= ![]() a,GC=3a.
a,GC=3a.
故计算出四边形GAFC的周长为5a+ ![]() a.
a.
【解析】(1)连接OC,根据切线的性质得到CG⊥OC.根据垂径定理即可得到结论;(2)连接AC,根据平行线的性质得到∠CGB=30°,推出△AOC是等边三角形,根据等边三角形的性质得到∠CAF=∠ACF=30°,CF=AF=a,DF= ![]() ,根据相似三角形的性质得到AG=
,根据相似三角形的性质得到AG= ![]() a,GC=3a.于是得到结论.
a,GC=3a.于是得到结论.
【考点精析】利用垂径定理和切线的性质定理对题目进行判断即可得到答案,需要熟知垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目