题目内容
【题目】在直角坐标系中，已知点A（﹣2，0），B（0，4），C（0，3），过点C作直线交x轴于点D，使得以D，O，C为顶点的三角形与△AOB相似，求点D的坐标．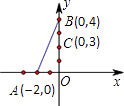 
【答案】解：过C点作AB的平行线，交x轴于D1点， 则△DOC∽△AOB， 
，
即 
，解得OD= 
，
∴D1（﹣ ，0），根据对称得D2（ ，0）；
由△COD∽△AOB，得D3（﹣6，0），根据对称得D4（6，0）．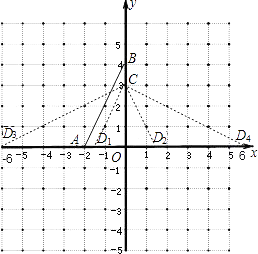
【解析】过C点作AB的平行线，交x轴于D1点，由平行得相似可知D1点符合题意，根据对称得D2点；改变相似三角形的对应关系得D3点，利用对称得D4点，都满足题意．
【考点精析】认真审题，首先需要了解相似三角形的判定(相似三角形的判定方法:两角对应相等，两三角形相似（ASA）；直角三角形被斜边上的高分成的两个直角三角形和原三角形相似； 两边对应成比例且夹角相等，两三角形相似（SAS）；三边对应成比例，两三角形相似（SSS）)．
练习册系列答案
相关题目
