Question

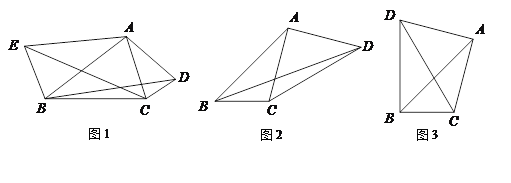
【题目】已知：如图，在△ABC中，AB=AC，D为边BC上一点，以AB，BD为邻边作平行四边形ABDE，连接AD，EC．

（1）求证：△ADC≌△ECD；

（2）当点D在什么位置时，四边形ADCE是矩形，请说明理由．

Answer 1

【答案】（1）证明见解析；

（2）点D在BC的中点上时，四边形ADCE是矩形．

【解析】

试题分析：（1）利用等边对等角以及平行四边形的性质可以证得∠EDC=∠ACB，则易证△ADC≌△ECD，利用全等三角形的对应边相等即可证得；

（2）根据平行四边形性质推出AE=BD=CD，AE∥CD，得出平行四边形，根据AC=DE推出即可．

试题解析：（1）证明：∵AB=AC，∴∠B=∠ACB，又∵ABDE中，AB=DE，AB∥DE，

∴∠B=∠EDC=∠ACB，AC=DE，

在△ADC和△ECD中，，

∴△ADC≌△ECD（SAS）．

（2）点D在BC的中点上时，四边形ADCE是矩形，∵四边形ABDE是平行四边形，

∴AE=BD，AE∥BC，∵D为边长中点，∴BD=CD，∴AE=CD，AE∥CD，

∴四边形ADCE是平行四边形，∵△ADC≌△ECD，∴AC=DE，

∴四边形ADCE是矩形，即点D在BC的中点上时，四边形ADCE是矩形．