题目内容
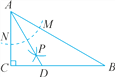
【题目】如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于点E,∠ADC+∠ABC=180°,有下列结论:①CD=CB;②AD+AB=2AE;③∠ACD=∠BCE;④AB-AD=2BE.其中正确的是( )

A. ② B. ①②③ C. ①②④ D. ①②③④
【答案】C
【解析】试题解析:在EA上取点EF=BE,连接CF,
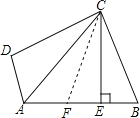
∵CE⊥AB,
∴CF=CB,
∴∠CFB=∠B,
∵∠AFC+∠CFB=180°,∠ADC+∠ABC=180°,
∴∠D=∠AFC,
∵AC平分∠BAD,
即∠DAC=∠FAC,
在△ACD和△ACF中,
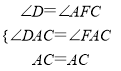 ,
,
∴△ACD≌△ACF(AAS),
∴CD=CF,
∴CD=CB,
故①正确;
∴AD=AF,
∴AD+AB=AF+AE+BE=AF+EF+AE=AE+AE=2AE.
故②正确;
根据已知条件无法证明∠ACD=∠BCE,
故③错误;
AB-AD=AB-AF=BF=2BE,
故④正确.
其中正确的是①②④.
故选C.

练习册系列答案
相关题目