题目内容
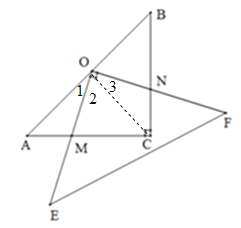
【题目】如图，在Rt△ACB中，AC=BC=8，O为AB的中点，以O为直角顶点作等腰直角三角形OEF,与边AC，BC相交于点M，N.有下列结论：①AM=CN；②CM+CN=8；③
；④当M是AC的中点时，OM=ON.其中正确结论的序号是______.
【答案】①②④
【解析】
连接OC．由等腰直角三角形的性质得到AO=BO=OC，∠A=∠ACO=∠OCB=45°，OC⊥AO，再由同角的余角相等，得到∠1=∠3，根据ASA即可证明△AMO≌△CNO，根据全等三角形的性质即可得到结论．
连接OC．
∵Rt△ACB中，AC=BC=8，O为AB的中点，∴AO=BO=OC，∠A=∠ACO=∠OCB=45°，OC⊥AO，∴∠1+∠2=90°．
∵∠EOF=90°，∴∠2+∠3=90°，∴∠1=∠3．
在△AMO和△CNO中，∵∠A=∠OCN=45°，AO=CO，∠1=∠3，∴△AMO≌△CNO，∴AM=CN，故①正确；
∵AM=CN，∴CM+CN=CM+AM=AC=8，故②正确；
∵△AMO≌△CNO，∴S△AMO=S△CNO，∴S四边形OMCN=S△OMC+S△CON= S△OMC+S△AOM=S△AOC=
S△ABC=
×AC×BC=×8×8=16，故③错误；
∵△AMO≌△CNO，∴MO=NO，故④正确．
故答案为：①②④．
练习册系列答案
相关题目
