Question

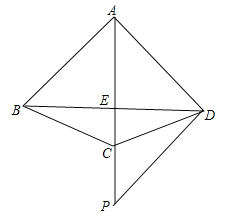
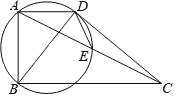
【题目】如图，四边形ABCD中，AD∥BC，∠ABC=90°，AB=5，BC=10，连接AC、BD，以BD为直径的圆交AC于点E．若DE=3，则AD的长为________.

Answer 1

【答案】2

【解析】

先证明△ADF∽△CAB，利用相似三角形的性质可得.再证明△DEF∽△DBA，利用相似三角形的性质可得，据此可求出DF的值，进而求出AD的值.

如图所示，过点D作DF⊥AC于点F，

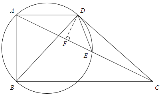
则∠AFD=∠CBA=90°.

∵AD∥BC，

∴∠DAF=∠ACB，

∴△ADF∽△CAB，

∴DF:AB=AD:CA。

在Rt△ABC中，AB=5，BC=10，

∴AC=，

∴，

∴.

在Rt△ABD中，.

∵同弧所对的圆周角相等，

∴∠DEF=∠DBA，

又∵∠DFE=∠DAB=90°，

∴△DEF∽△DBA，

∴，即，

∴DF=2，

∴AD=2.

故答案为：2.