Question

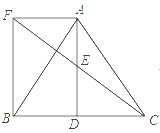
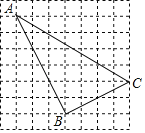
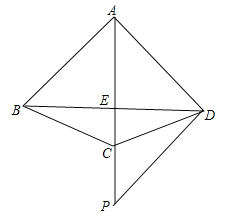
【题目】（2017山东省泰安市）如图，四边形ABCD中，AB=AC=AD，AC平分∠BAD，点P是AC延长线上一点，且PD⊥AD．

（1）证明：∠BDC=∠PDC；

（2）若AC与BD相交于点E，AB=1，CE：CP=2：3，求AE的长．

Answer 1

【答案】（1）证明见解析；（2）．

【解析】试题（1）直接利用等腰三角形的性质结合互余的定义得出∠BDC=∠PDC；

（2）首先过点C作CM⊥PD于点M，进而得出△CPM∽△APD，求出EC的长即可得出答案．

试题解析：解：（1）∵AB=AD，AC平分∠BAD，∴AC⊥BD，∴∠ACD+∠BDC=90°．∵AC=AD，∴∠ACD=∠ADC，∴∠ADC+∠BDC=90°．∵PD⊥AD，∴∠ADC+∠PDC=90°，∴∠BDC=∠PDC；

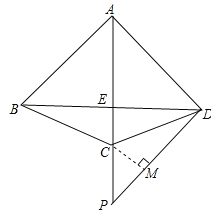
（2）过点C作CM⊥PD于点M，∵∠BDC=∠PDC，∴CE=CM，∵∠CMP=∠ADP=90°，∠P=∠P，∴△CPM∽△APD，∴，设CM=CE=x，∵CE：CP=2：3，∴PC=x，∵AB=AD=AC=1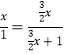，∴，解得：x=，故AE=1﹣=．