题目内容
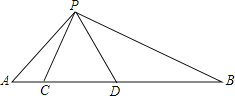
【题目】如图,点C、D在线段AB上,△PCD是等边三角形,且△ACP∽△PDB.
(1)求∠APB的大小.
(2)说明线段AC、CD、BD之间的数量关系.
【答案】(1)120°;(2)见解析
【解析】
(1)根据等边三角形的性质得到∠PCD=60°,根据相似三角形的性质得到∠APC=∠PBD,根据三角形内角和定理计算;
(2)根据相似三角形的性质、等边三角形的性质解答.
解:(1)∵△PCD是等边三角形,
∴∠PCD=60°,
∴∠A+∠APC=60°,
∵△ACP∽△PDB,
∴∠APC=∠PBD,
∴∠A+∠B=60°,
∴∠APB=120°;
(2)∵△PCD是等边三角形,
∴PC=PD=CD,
∵△ACP∽△PDB,
∴![]() =
=![]() ,
,
∴CD2=ACBD.

练习册系列答案
相关题目