题目内容
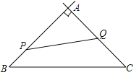
【题目】如图,![]() ,
,![]() ,点D在边BC上
,点D在边BC上![]() 与B、C不重合
与B、C不重合![]() ,四边形ADEF为正方形,过点F作
,四边形ADEF为正方形,过点F作![]() ,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:
,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:![]() ;
;![]() :
:![]() :2;
:2;![]() ;
;![]() ,其中正确的结论的个数是()
,其中正确的结论的个数是()

A.1B.2C.3D.4
【答案】D
【解析】
由正方形的性质得出∠FAD=90°,AD=AF=EF,证出∠CAD=∠AFG,由AAS证明△FGA≌△ACD,得出AC=FG,①正确;
证明四边形CBFG是矩形,得出S△FAB=![]() FBFG=
FBFG=![]() S四边形CBFG,②正确;
S四边形CBFG,②正确;
由等腰直角三角形的性质和矩形的性质得出∠ABC=∠ABF=45°,③正确;
证出△ACD∽△FEQ,得出对应边成比例,得出DFE=AD2=FQAC,④正确.
解:∵四边形ADEF为正方形,
∴∠FAD=90°,AD=AF=EF,
∴∠CAD+∠FAG=90°,
∵FG⊥CA,
∴∠GAF+∠AFG=90°,
∴∠CAD=∠AFG,
在△FGA和△ACD中,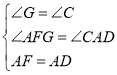
∴△FGA≌△ACD(AAS),
∴AC=FG,①正确;
∵BC=AC,
∴FG=BC,
∵∠ACB=90°,FG⊥CA,
∴FG∥BC,
∴四边形CBFG是矩形,
∴∠CBF=90°,S△FAB=![]() FBFG=
FBFG=![]() S四边形CBFG,②正确;
S四边形CBFG,②正确;
∵CA=CB,∠C=∠CBF=90°,
∴∠ABC=∠ABF=45°,③正确;
∵∠FQE=∠DQB=∠ADC,∠E=∠C=90°,
∴△ACD∽△FEQ,
∴AC:AD=FE:FQ,
∴ADFE=AD2=FQAC,④正确;
所以①②③④正确.
故选:D.

练习册系列答案
相关题目