题目内容
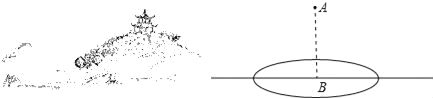
【题目】如图,要建一个面积为140平方米的仓库,仓库的一边靠墙,这堵墙长16米;在与墙平行的一边,要开一扇2米宽的门.已知围建仓库的现有木板材料可使新建板墙的总长为32米,那么这个仓库设计的长和宽应分别为多少米?

【答案】仓库的长和宽分别为14米,10米.
【解析】
设垂直于墙的一边长为x米,则平行于墙的一边长为(32-2x+2)米,根据矩形面积公式可列出方程,求出答案.
设垂直于墙的一边长为x米,则平行于墙的一边长为(32-2x+2)米,
由题意得x(32-2x+2)=140,
整理,得x2-17x+70=0,
解得x1=10,x2=7,
当垂直于墙的边长为7米,则平行于墙的长度为32-14+2=20(米)>16米,舍去;
当垂直于墙的边长为10米,则平行于墙的长度为32-20+2=14(米);
答:仓库的长和宽分别为14米,10米.

练习册系列答案
相关题目