题目内容
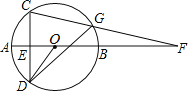
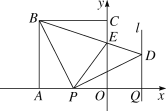
【题目】如图,已知BD⊥AB于点B,AC⊥AB于点A,且BD=3,AC=2,AB=m,在线段AB上找一点E,使△BDE与△ACE相似,若这样的点E有且只有两个,则m的值是______
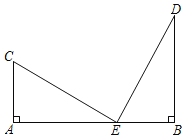
【答案】5或2![]()
【解析】
当∠ACE=∠BDE时,△ACE∽△BDE,得出![]() ,AE=
,AE=![]() BE①,当ACE=∠BED时,△ACE∽△BED,得出
BE①,当ACE=∠BED时,△ACE∽△BED,得出![]() ,即AE×BE=AC×BD=6②,由①②得出
,即AE×BE=AC×BD=6②,由①②得出![]() BE2=6,解得BE=3,AE=2,得出m=5;当AE=2时,BE=3,两个三角形相似;当AE=3时,BE=2,两个三角形全等,符合题目要求;设AE=x,则BE=m﹣x,得出x:3=2:(m﹣x),整理得x2﹣mx+6=0,方程有唯一解时,△=m2﹣24=0,解得m=
BE2=6,解得BE=3,AE=2,得出m=5;当AE=2时,BE=3,两个三角形相似;当AE=3时,BE=2,两个三角形全等,符合题目要求;设AE=x,则BE=m﹣x,得出x:3=2:(m﹣x),整理得x2﹣mx+6=0,方程有唯一解时,△=m2﹣24=0,解得m=![]() ,当m=
,当m=![]() 时,AE:BE=2:3时,两个三角形相似;AE=BE=
时,AE:BE=2:3时,两个三角形相似;AE=BE=![]() 时,两个三角形相似;同样是两个点可以满足要求;即可得出答案.
时,两个三角形相似;同样是两个点可以满足要求;即可得出答案.
解:∵BD⊥AB于点B,AC⊥AB,
∴∠A=∠B=90°,
当∠ACE=∠BDE时,△ACE∽△BDE,
∴![]() ,
,
∴AE=![]() BE①,
BE①,
当ACE=∠BED时,△ACE∽△BED,
∴![]() ,即AE×BE=AC×BD=2×3=6②,
,即AE×BE=AC×BD=2×3=6②,
由①②得:![]() BE2=6,
BE2=6,
解得:BE=3,
∴AE=2,
∴AB=AE+BE=5,即m=5;
当AE=2时,BE=3,两个三角形相似;
当AE=3时,BE=2,两个三角形全等,符合题目要求;
设AE=x,则BE=m﹣x,
∴x:3=2:(m﹣x),
整理得:x2﹣mx+6=0,
方程有唯一解时,△=m2﹣24=0,
解得:m=±![]() (负值舍去),
(负值舍去),
∴m=![]() ;
;
当m=![]() 时,
时,
AE:BE=2:3时,两个三角形相似;
AE=BE=![]() 时,两个三角形相似;同样是两个点可以满足要求;
时,两个三角形相似;同样是两个点可以满足要求;
综上所述,△BDE与△ACE相似,若这样的点E有且只有两个,则m的值是5或![]() ;
;
故答案为:5或![]() .
.

【题目】东坡商贸公司购进某种水果成本为20元/![]() ,经过市场调研发现,这种水果在未来48天的销售单价
,经过市场调研发现,这种水果在未来48天的销售单价![]() (元/
(元/![]() )与时间
)与时间![]() (天)之间的函数关系式
(天)之间的函数关系式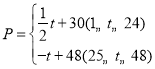 ,
,![]() 为整数,且其日销售量
为整数,且其日销售量![]() (
(![]() )与时间
)与时间![]() (天)的关系如下表:
(天)的关系如下表:
时间 | 1 | 3 | 6 | 10 | 20 | … |
日销售量 | 118 | 114 | 108 | 100 | 80 | … |
(1)已知![]() 与
与![]() 之间的变化符合一次函数关系,试求在第30天的日销售量;
之间的变化符合一次函数关系,试求在第30天的日销售量;
(2)哪一天的销售利润最大?最大日销售利润为多少?