题目内容
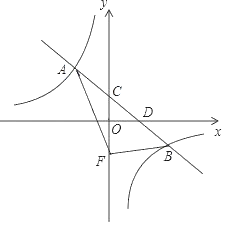
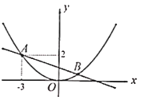
【题目】如图1,在平面直角坐标系中,抛物线y=ax2﹣2x﹣3a与x轴交于A、B两点,与y轴交于C点,OC=OB,点P为抛物线上一动点
(1)求抛物线的解析式;
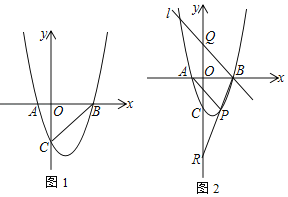
(2)当点P运动到抛物线对称轴右侧时如图2,连PC、BC、BP得△BCP.设△BCP的面积为s,点P的横坐标为x.若s<![]() ,求x的取值范围;
,求x的取值范围;
(3)当点P运动到第四象限时,连AP、BP,BP交y轴于点R,过B作直线l∥AP交y轴于点Q,问:QR、OC之间是否存在确定的数量关系?若存在,请求出并证明;若不存在,请说明理由.
【答案】(1)y=x2﹣2x﹣3;(2)1<x<![]() 且x≠
且x≠![]() ;(3)存在,RQ=4OC,见解析
;(3)存在,RQ=4OC,见解析
【解析】
(1)由已知可求A(﹣1,0),B(3,0),C(0,﹣3),所以﹣3a=﹣3,即a=1;
(2)当点P在x轴下方时,设P(x,x2﹣2x﹣3),过点P作PQ∥y轴,交BC于点Q,求得直线BC的解析式为y=x﹣3,所以Q(x,x﹣3),表示出S![]() ,当S=
,当S=![]() 时,
时,![]() ,当点P在x轴上时,同理可得,
,当点P在x轴上时,同理可得,![]() 时,
时,![]() ;由已知并结合图象可得,1<x<
;由已知并结合图象可得,1<x<![]() 且x≠
且x≠![]() ;
;
(3)设直线AP的解析式为y=kx+k,联立方程组![]() ,可得xp=3+k,设直线BP的解析式为y=mx﹣3m,联立方程组
,可得xp=3+k,设直线BP的解析式为y=mx﹣3m,联立方程组![]() ,可得xp+3=m+2,则有m﹣k=4,设直线BQ的解析式为y=kx﹣3k,分别得到Q(0,﹣3k),R(0.﹣3m),则可得RQ=4OC.
,可得xp+3=m+2,则有m﹣k=4,设直线BQ的解析式为y=kx﹣3k,分别得到Q(0,﹣3k),R(0.﹣3m),则可得RQ=4OC.
(1)由已知可求A(﹣1,0),B(3,0),
∵OC=OB,
∴C(0,﹣3),
∴﹣3a=﹣3,
∴a=1,
∴y=x2﹣2x﹣3;
(2)当点P在x轴下方时,设P(x,x2﹣2x﹣3),过点P作PQ∥y轴,交BC于点Q,
求得直线BC的解析式为y=x﹣3,
∴Q(x,x﹣3),
∴![]() ,即
,即![]() ,
,
当S=![]() 时,
时,![]() ,
,
化简得:![]() ,即:
,即:![]() ,
,
∴![]() ,
,
当点P在x轴上时,同理可得,
![]() 时,
时,![]() ;
;
∵P点在对称轴的右侧,
∴当S<![]() 时,由图象可得,1<x<
时,由图象可得,1<x<![]() 且x≠
且x≠![]() ;
;
(3)设直线AP的解析式为![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵点![]() 的坐标为:(﹣1,0),
的坐标为:(﹣1,0),
∴-1是方程的一个根,
∴xp+(﹣1)=2+k,xp=3+k,
设直线BP的解析式为y=mx﹣3m,
∴![]() ,
,
∴![]() ,
,
∵点![]() 的坐标为:(3,0),
的坐标为:(3,0),
∴xp+3=m+2,xp=m-1,
∴3+k=m﹣1,
∴m﹣k=4,
设直线BQ的解析式为y=kx﹣3k,
∴Q(0,﹣3k),
∵R(0,﹣3m),
∴RQ=﹣3k+3m=12,
∵CO=3,
∴RQ=4OC.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案