题目内容
如图，⊙O1与⊙O2相交于A、B两点，经过点A的直线CD分别与⊙O1、⊙O2交于C、D，经过点B的直线EF分别与⊙O1、⊙O2交于E、F，且EF∥O1O2．下列结论：①CE∥DF；②∠D=∠F；③EF=2O1O2．必定成立的有（ ）
A．0个
B．1个
C．2个
D．3个
【答案】分析：根据相交两圆的性质、圆周角定理的推论、平行线的判定以及三角形的中位线定理分别判断．
解答：
解：连接AB，AE，AF，根据相交两圆的连心线垂直平分两圆的公共弦，得AB⊥01O2．再根据90°的圆周角所对的弦是直径，得AE，AF是直径．
①、根据直径所对的圆周角是直角，得∠C=∠D=90°，则∠C+∠D=180°，得CE∥DF；
②、因为BD不一定是直径，所以∠F不一定是直角，错误；
③、根据三角形的中位线定理，得EF=2O1O2．
故选C．
点评：考查了相交两圆的性质、圆周角定理的推论、平行线的判定以及三角形的中位线定理．
解答：
解：连接AB，AE，AF，根据相交两圆的连心线垂直平分两圆的公共弦，得AB⊥01O2．再根据90°的圆周角所对的弦是直径，得AE，AF是直径．①、根据直径所对的圆周角是直角，得∠C=∠D=90°，则∠C+∠D=180°，得CE∥DF；
②、因为BD不一定是直径，所以∠F不一定是直角，错误；
③、根据三角形的中位线定理，得EF=2O1O2．
故选C．
点评：考查了相交两圆的性质、圆周角定理的推论、平行线的判定以及三角形的中位线定理．
练习册系列答案
相关题目
12、已知：如图，⊙O1与⊙O2外切于点P，直线AB过点P交⊙O1于A，交⊙O2于B，点C、D分别为⊙O1、⊙O2上的点，且∠ACP=65°，则∠BDP=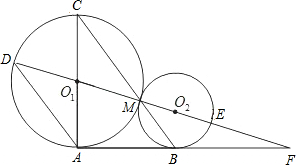
已知：如图，⊙O1与⊙O2外切于M点，AF是两圆的外公切线，A、B是切点，DF经过O1、O2，分别交⊙O1于D、⊙O2于E，AC是⊙O1的直径，BC经过M点，连接AD．
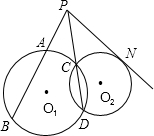如图，⊙O1与⊙O2相交于C、D两点，⊙O1的割线PAB与DC的延长线交于点P，PN与⊙O2相切于点N，若PB=10，AB=6，则PN=
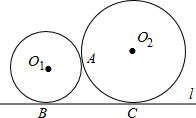已知：如图，⊙O1与⊙O2外切于A点，直线l与⊙O1、⊙O2分别切于B，C点，若⊙O1的半径r1=2cm，⊙O2的半径r2=3cm．求BC的长．
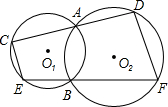已知如图：⊙O1与⊙O2相交于AB两点，过点A、B的直线分别与⊙O1交于C、E，与⊙O2交于D、F，连接CE、DF．