题目内容
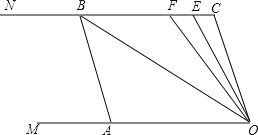
【题目】如图,点B、E分别在直线AC和DF上,若∠AGB=∠EHF,∠C=∠D,可以证明∠A=∠F.请完成下面证明过程中的各项“填空”.

证明:∵∠AGB=∠EHF(理由: )
∠AGB= (对顶角相等)
∴∠EHF=∠DGF,∴DB∥EC(理由: )
∴ =∠DBA(两直线平行,同位角相等)
又∵∠C=∠D,∴∠DBA=∠D,
∴DF∥ (内错角相等,两直线平行)
∴∠A=∠F(理由: ).
【答案】已知;∠DGF;同位角相等,两直线平行;∠C; AC;∠A=∠F.
【解析】
分析: 根据对顶角相等推知同位角∠EHF=∠DGF,从而证得两直线DB∥EC;然后由平行线的性质知内错角∠DBA=∠D,即可根据平行线的判定定理推知两直线DF∥AC;最后由平行线的性质(两直线平行,内错角相等)证得∠A=∠F.
详解: ∵∠AGB=∠EHF(已知),∠AGB=∠DGF(对顶角相等),
∴∠EHF=∠DGF
∴DB∥EC(同位角相等,两直线平行),
∴∠C=∠DBA(两直线平行,同位角相等),
又∵∠C=∠D(已知),
∴∠DBA=∠D(等量代换),
∴DF∥AC(内错角相等,两直线平行),
∴∠A=∠F(两直线平行,内错角相等),
故答案是:已知;∠DGF;同位角相等,两直线平行;C;AC;两直线平行,内错角相等.

练习册系列答案
相关题目