题目内容
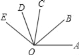
【题目】如图,已知两条射线OM∥CN,动线段AB的两个端点A、B分别在射线OM、CN上,且∠C=∠OAB=108°,F在线段CB上,OB平分∠AOF,OE平分∠COF.
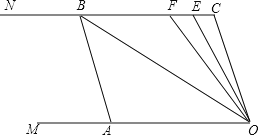
(1)请在图中找出与∠AOC相等的角,并说明理由;
(2)若平行移动AB,那么∠OBC与∠OFC的度数比是否随着AB位置的变化而发生变化?若变化,找出变化规律;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=2∠OBA?若存在,请求出∠OBA度数;若不存在,说明理由.
【答案】(1)∠ABC,∠BAM;理由见解析.(2)不变,![]() ;(3)不存在.
;(3)不存在.
【解析】
试题分析:(1)根据两直线平行,同旁内角互补可得求出∠ABC,再根据邻补角的定义求出∠BAM即可得解;
(2)根据两直线平行,内错角相等可得∠OBC=∠AOB,∠OFC=∠AOF,再根据角平分线的定义可得∠AOF=2∠AOB,从而得到比值不变;
(3)设∠OBA=x,表示出∠OEC,然后利用三角形的内角和定理表示出∠AOB、∠COE,再根据角平分线的定义根据∠AOB+∠COE=![]() ∠AOC列出方程求解即可.
∠AOC列出方程求解即可.
试题解析:(1)∵OM∥CN,
∴∠AOC=180°-∠C=180°-108°=72°,
∠ABC=180°-∠OAB=180°-108°=72°,
又∵∠BAM=∠180°-∠OAB=180°-108°=72°,
∴与∠AOC相等的角是∠ABC,∠BAM;
(2)∵OM∥CN,
∴∠OBC=∠AOB,∠OFC=∠AOF,
∵OB平分∠AOF,
∴∠AOF=2∠AOB,
∴∠OFC=2∠OBC,
∴∠OBC:∠OFC=![]() ;
;
(3)设∠OBA=x,则∠OEC=2x,
在△AOB中,∠AOB=180°-∠OAB-∠ABO=180°-x-108°=72°-x,
在△OCE中,∠COE=180°-∠C-∠OEC=180°-108°-2x=72°-2x,
∵OB平分∠AOF,OE平分∠COF,
∴∠COE+∠AOB=![]() ∠COF+
∠COF+![]() ∠AOF=
∠AOF=![]() ∠AOC=
∠AOC=![]() ×72°=36°,
×72°=36°,
∴72°-x+72°-2x=36°,
解得x=36°,
即∠OBA=36°,
此时,∠OEC=2×36°=72°,
∠COE=72°-2×36°=0°,
点C、E重合,
所以,不存在.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案