题目内容
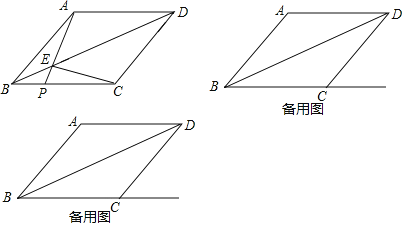
【题目】如图,菱形ABCD中,AB=20,连接BD,点P是射线BC上一点(不与点B重合),AP与对角线BD交于点E,连接EC.
(1)求证:AE=CE;
(2)若sin∠ABD=![]() ,当点P在线段BC上时,若BP=8,求△PEC的面积;
,当点P在线段BC上时,若BP=8,求△PEC的面积;
(3)若∠ABC=45°,当点P在线段BC的延长线上时,请求出△PEC是等腰三角形时BP的长.
【答案】(1)见解析;(2)![]() ;(3)20
;(3)20![]() 或10
或10![]() +10
+10![]()
【解析】
(1)由SAS证得△ABE≌△CBE,即可得出结论;
(2)连接AC,交BD于O,求出OA=4![]() ,OB=8
,OB=8![]() ,则AC=8
,则AC=8![]() ,BD=16
,BD=16![]() ,S菱形ABCD=320,S△ABC=160,
,S菱形ABCD=320,S△ABC=160,![]() ,则S△ABP=
,则S△ABP=![]() S△ABC=64,易证∠ABE=∠PBE,得出
S△ABC=64,易证∠ABE=∠PBE,得出![]() ,则S△BPE=
,则S△BPE=![]() S△ABP=
S△ABP=![]() ,由
,由![]() ,得出S△PEC=
,得出S△PEC=![]() S△BPE即可得出结果;
S△BPE即可得出结果;
(3)①由(1)得△ABE≌△CBE,则∠BAE=∠BCE,当∠BAE=90°时,得△PEC是等腰直角三角形,过点E作∠FEC=45°交BC于F,则△FCE为等腰直角三角形,得出CE=CP=CF,EF=![]() CF,证明∠BEF=∠EBC,得出EF=BF,则
CF,证明∠BEF=∠EBC,得出EF=BF,则![]() CF+CF=BC=20,求出CF=20(
CF+CF=BC=20,求出CF=20(![]() ﹣1),即可得出结果;
﹣1),即可得出结果;
②由(1)得△ABE≌△CBE,则∠AEB=∠CEB,当∠BAE=105°时,∠AEB=52.5°,得出∠AEC=105°,∠CEP=75°,证明∠ECP=∠CEP,得出△PEC是等腰三角形,过点A作AN⊥BP于N,则△ABN是等腰直角三角形,得出AN=BN=![]() AB=10
AB=10![]() ,由tan30°=
,由tan30°=![]() ,求出PN=10
,求出PN=10![]() ,即可得出结果.
,即可得出结果.
(1)证明:∵四边形ABCD是菱形,
∴∠ABE=∠CBE,AB=BC,
在△ABE和△CBE中,
 ,
,
∴△ABE≌△CBE(SAS),
∴AE=CE;
(2)解:连接AC,交BD于O,如图1所示:
∵四边形ABCD是菱形,
∴∠AOB=90°,OB=OD,OA=OC,AB=BC=20,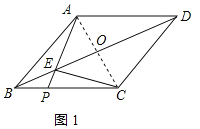
∵sin∠ABD=![]() ,
,
∴OA=4![]() ,
,
∴AC=2OA=2×4![]() =8
=8![]() ,
,
BD=2OB=2×8![]() =16
=16![]() ,
,
∴S菱形ABCD=![]() ACBD=
ACBD=![]() ×8
×8![]() ×16
×16![]() =320,
=320,
∴S△ABC=![]() S菱形ABCD=
S菱形ABCD=![]() ×320=160,
×320=160,
∵BP=8,
∴CP=BC-BP=20-8=12,
∵![]() ,
,
∴S△ABP=![]() S△ABC=
S△ABC=![]() ×160=64,
×160=64,
∵四边形ABCD是菱形,
∴∠ABE=∠PBE,
∴点E到边AB、BP的距离相等,
∴![]() ,
,
∴S△BPE=![]() S△ABP=
S△ABP=![]() ×64=
×64=![]() ,
,
∵![]() ,
,
∴S△PEC=![]() S△BPE=
S△BPE=![]() ×
×![]() =
=![]() ;
;
(3)解:①由(1)得:△ABE≌△CBE,
∴∠BAE=∠BCE,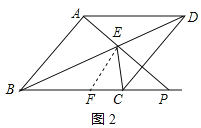
当∠BAE=90°时,则∠BCE=90°,
∴∠ECP=90°,
∵∠ABC=45°,
∴∠EBC=22.5°,∠CPE=45°,
∴△PEC是等腰直角三角形,
∴CE=CP,∠BEC=90°-22.5°=67.5°,
过点E作∠FEC=45°交BC于F,如图2所示:
则△FCE为等腰直角三角形,
∴CE=CP=CF,EF=![]() CF,∠BEF=∠BEC-∠FEC=67.5°-45°=22.5°,
CF,∠BEF=∠BEC-∠FEC=67.5°-45°=22.5°,
∴∠BEF=∠EBC,
∴EF=BF,
∴![]() CF+CF=BC=20,
CF+CF=BC=20,
∴CF=![]() =20(
=20(![]() -1),
-1),
∴BP=BC+CP=BC+CF=20+20(![]() -1)=20
-1)=20![]() ;
;
②由(1)得:△ABE≌△CBE,
∴∠AEB=∠CEB,
当∠BAE=105°时,∠AEB=180°-105°-22.5°=52.5°,
∴∠AEC=2∠AEB=105°,
∴∠CEP=180°-105°=75°,
∵∠APB=180°-105°-45°=30°,
∴∠ECP=180°-75°-30°=75°,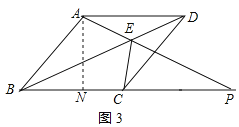
∴∠ECP=∠CEP,
∴△PEC是等腰三角形,
过点A作AN⊥BP于N,如图3所示:
则△ABN是等腰直角三角形,
∴AN=BN=![]() AB=10
AB=10![]() ,
,
∵∠APB=30°,
∴tan30°=![]() ,即
,即![]() ,
,
∴PN=10![]() ,
,
∴BP=BN+PN=10![]() +10
+10![]() ;
;
综上所述,△PEC是等腰三角形时BP的长为20![]() 或10
或10![]() +10
+10![]() .
.

【题目】如图,在Rt△ABC中,∠ACB=90°.∠ABC的平分线交AC于点O,以点O为圆心,OC为半径.在△ABC同侧作半圆O.
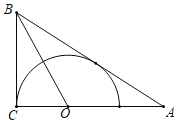
(1)求证:AB与⊙O相切;
(2)若AB=5,AC=4,求⊙O的半径.
【题目】某电器商场销售每台进价分别为400元、340元的A、B两种型号的电风扇,下表是该型号电风扇近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 3600元 |
第二周 | 4台 | 10台 | 6200元 |
(1)求A、B两种型号的电风扇的销售单价;
(2)若该商场准备用不多于1.14万元的金额再采购这两种型号的电风扇共30台,假设售价不变,那么商场应采用哪种采购方案,才能使得当销售完这些风扇后,商场获利最多?最多可获利多少元?
【题目】如图,AB∥CD,AB=5cm,AC=4cm,线段AC上有一动点E,连接BE,ED,∠BED=∠A=60°,设A,E两点间的距离为xcm,C,D两点间的距离为ycm.
小明根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小明的探究过程,请补充完整.
(1)列表:如表的已知数据是根据A,E两点间的距离x进行取点、画图、测量,分别得到了x与y的几组对应值:
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.3 | 2.5 |
y/cm | 0 | 0.39 | 0.75 | 1.07 | 1.33 | 1.45 |
|
x/cm | 2.8 | 3.2 | 3.5 | 3.6 | 3.8 | 3.9 | |
y/cm | 1.53 | 1.42 | 1.17 | 1.03 | 0.63 | 0.35 |
请你补全表格;
(2)描点、连线:在平面直角坐标系xOy中,描出表中各组数值所对应的点(x,y),并画出函数y关于x的图象;
(3)探究性质:随着自变量x的不断增大,函数y的变化趋势: ;
(4)解决问题:当AE=2CD时,CD的长度大约是 cm.