��Ŀ����
����Ŀ��ij�����̳�����ÿ̨���۷ֱ�Ϊ400Ԫ��340Ԫ��A��B�����ͺŵĵ���ȣ��±��Ǹ��ͺŵ���Ƚ����ܵ����������
����ʱ�� | �������� | �������� | |
A���ͺ� | B���ͺ� | ||
��һ�� | 3̨ | 5̨ | 3600Ԫ |
�ڶ��� | 4̨ | 10̨ | 6200Ԫ |
��1����A��B�����ͺŵĵ���ȵ����۵��ۣ�
��2�������̳����ò�����1.14��Ԫ�Ľ���ٲɹ��������ͺŵĵ���ȹ�30̨�������ۼ۲��䣬��ô�̳�Ӧ�������ֲɹ�����������ʹ�õ���������Щ���Ⱥ��̳�������ࣿ���ɻ�������Ԫ��
���𰸡���1��A���ͺŵ�������۵���Ϊ500Ԫ/̨��B���ͺŵ�������۵���Ϊ420Ԫ/̨����2������A���ͺŷ���20̨��B���ͺŷ���10̨���ɻ�����࣬���ɻ���2800Ԫ
��������
(1)�ȸ��ݵ�һ�ܺ͵ڶ��ܵ������ͺŵĵ���ȵ����������г���Ԫһ�η����飬����⼴�ɵõ��𰸣�
(2)�蹺��A���ͺŵ����ą���������ֵ���ȵĽ��۲�����1.14��Ԫ�����a��ȡֵ��Χ�����������������һ�κ��������������ֵ���ɣ�
�⣺��A���ͺŵ�������۵���ΪxԪ/̨��B���ͺŵ�������۵���ΪyԪ/̨��
����֪��![]() ����ã�
����ã�![]()
��A���ͺŵ�������۵���Ϊ500Ԫ/̨��B���ͺŵ�������۵���Ϊ420Ԫ/̨��
��2���⣺�赱����A���ͺŵ����ąʱ������õ�����ΪwԪ��������ã�
![]()
��ã�![]() ��
��
��w����500��400��a+��420��340����30��a����20a+2400��
�֡�20��0��
��a��ֵ����ʱ��w��ֵҲ����
�൱a��20ʱ��wȡ�����ֵ����ʱw��20��20+2400��2800�����̳�Ӧ���õĽ�������Ϊ������A���ͺŷ���20̨��B���ͺŷ���10̨���ɻ�����࣬���ɻ���2800Ԫ��

 �¿α�ͬ��ѵ��ϵ�д�
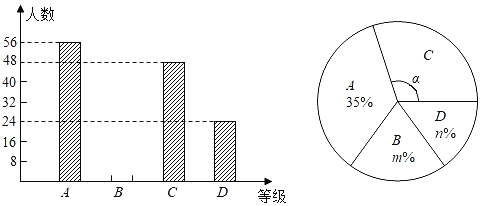
�¿α�ͬ��ѵ��ϵ�д�����Ŀ��Ϊӭ��2022�궬�»ᣬ��������Ĵ�ѧ�����뵽־Ը�����У��ס�������ѧУ��֯��־Ը�����Ŷ�ѡ�λ��������ѡ������ѧУ����300��ѧ�������ۺ�����չʾ���ڣ�Ϊ���˽���Щѧ�����������������У�����ۺ�����չʾ���ڵ�ѧ���зֱ������ȡ��50��ѧ�����ۺ�����չʾ�ɼ����ٷ��ƣ����������ݣ��ɼ������������������ͷ�������������˲�����Ϣ��
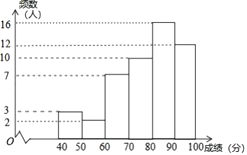
a����ѧУѧ���ɼ���Ƶ���ֲ�ֱ��ͼ��ͼ�����ݷֳ�6�飺![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����
����
b����ѧУѧ���ɼ���![]() ��һ���ǣ�
��һ���ǣ�
80 80 81 81.5 82 83 83 84
85 86 86.5 87 88 88.5 89 89
c����ѧУѧ���ɼ���ƽ��������λ���������������ʣ�85�ּ�����Ϊ���㣩���£�
ƽ���� | ��λ�� | ���� | ������ |
83.3 | 84 | 78 | 46% |
����������Ϣ���ش��������⣺
��1����ѧУѧ��![]() ����ѧУѧ��
����ѧУѧ��![]() ���ۺ�����չʾ�ɼ�ͬΪ82�֣��������ڱ�Уѧ�����ۺ�����չʾ��������ǰ����________���
���ۺ�����չʾ�ɼ�ͬΪ82�֣��������ڱ�Уѧ�����ۺ�����չʾ��������ǰ����________���![]() ����
����![]() ������
������
��2������������Ϣ���ƶ�________ѧУ�ۺ�����չʾ��ˮƽ���ߣ�����Ϊ��__________________________
�����ٴ�������ͬ�ĽǶ�˵���ƶϵĺ����ԣ���
��3����ÿ��ѧУ�ۺ�����չʾ��ǰ120��ѧ������ѡ��־Ը�����Ŷӣ�Ԥ����ѧУ�������ٴﵽ________�ֵ�ѧ���ſ�����ѡ��
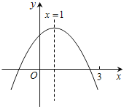
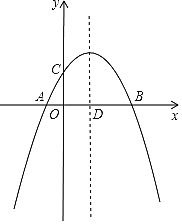
����Ŀ�����κ���y��ax2+bx+c��a��b��cΪ��������a��0���е�x��y�IJ��ֶ�Ӧֵ�����
x | ��1 | 0 | 1 | 3 |
y | ��1 | 3 | 5 | 3 |
���н��۴�����ǣ�������
A.ac��0
B.��x��1ʱ��y��ֵ��x���������С
C.3�Ƿ���ax2+��b��1��x+c��0��һ����
D.����1��x��3ʱ��ax2+��b��1��x+c��0