��Ŀ����
����Ŀ����ƽ��ֱ������ϵxOy�У���C�İ뾶Ϊr��P����Բ��C���غϵĵ㣬��P���ڡ�C�ķ��Ƶ�Ķ������£���������CP�ϴ���һ��P�䣬����CP+CP��=2r�����P��Ϊ��P���ڡ�C�ķ��Ƶ㣬��ͼΪ��P������ڡ�C�ķ��Ƶ�P���ʾ��ͼ��
�ر�أ�����P����Բ��C�غ�ʱ���涨CP��=0
��1������O�İ뾶Ϊ1ʱ��
�ٷֱ��жϵ�M��2��1����N��![]() ��0����T��1��
��0����T��1��![]() �����ڡ�O�ķ��Ƶ��Ƿ���ڣ������ڣ��������ꣻ
�����ڡ�O�ķ��Ƶ��Ƿ���ڣ������ڣ��������ꣻ
�ڵ�P��ֱ��y=��x+2�ϣ�����P���ڡ�O�ķ��Ƶ�P����ڣ��ҵ�P�䲻��x���ϣ����P�ĺ������ȡֵ��Χ��
��2����C��Բ����x���ϣ��뾶Ϊ1��ֱ��y=��![]() x+2
x+2![]() ��x�ᡢy��ֱ��ڵ�A��B�����߶�AB�ϴ��ڵ�P��ʹ�õ�P���ڡ�C�ķ��Ƶ�P���ڡ�C���ڲ�����Բ��C�ĺ������ȡֵ��Χ��
��x�ᡢy��ֱ��ڵ�A��B�����߶�AB�ϴ��ڵ�P��ʹ�õ�P���ڡ�C�ķ��Ƶ�P���ڡ�C���ڲ�����Բ��C�ĺ������ȡֵ��Χ��
���𰸡�
��1��
�⣺����O�İ뾶Ϊ1ʱ��
�ٵ�M��2��1�����ڡ�O�ķ��Ƶ㲻���ڣ�
N��![]() ��0�����ڡ�O�ķ��Ƶ���ڣ����Ƶ�N�䣨
��0�����ڡ�O�ķ��Ƶ���ڣ����Ƶ�N�䣨![]() ��0����
��0����
T��1��![]() �����ڡ�O�ķ��Ƶ���ڣ����Ƶ�T�䣨0��0����
�����ڡ�O�ķ��Ƶ���ڣ����Ƶ�T�䣨0��0����
�ڡ�OP��2r=2��OP2��4����P��x����x+2����
��OP2=x2+����x+2��2=2x2��4x+4��4��
��2x2��4x��0��
x��x��2����0��
��0��x��2��
��x=2ʱ��P��2��0����P�䣨0��0�����������⣻
��x=0ʱ��P��0��2����P�䣨0��0�����������⣻
��0��x��2��
��2��
�⣺��ֱ��y=��![]() x+2
x+2![]() ��x�ᡢy��ֱ��ڵ�A��B��
��x�ᡢy��ֱ��ڵ�A��B��
��A��6��0����B��0��2![]() ����
����
��![]() =
=![]() ��
��
���OBA=60�㣬��OAB=30�㣮
��C��x��0����
�ٵ�C��OA��ʱ����CH��AB��H��
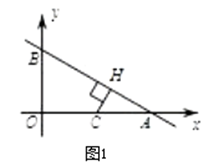
��CH��CP��2r=2��
����AC��2��
C�������x��2����x=2ʱ��C�����꣨2��0����H��ķ��Ƶ�H�䣨2��0����Բ���ڲ�����
�ڵ�C��A���Ҳ�ʱ��
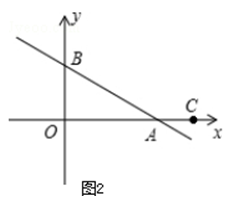
C���߶�AB�ľ���ΪAC����AC���ֵΪ8��
����C�������x��10��
����������Բ��C�ĺ������ȡֵ��Χ��2��x��8��
����������1���ٸ��ݷ��Ƶ�Ķ��壬�ɵõ���O�İ뾶Ϊ1ʱ����M��2��1�����ڡ�O�ķ��Ƶ㲻���ڣ�N��![]() ��0�����ڡ�O�ķ��Ƶ���ڣ����Ƶ�N�䣨
��0�����ڡ�O�ķ��Ƶ���ڣ����Ƶ�N�䣨![]() ��0����T��1��
��0����T��1��![]() �����ڡ�O�ķ��Ƶ���ڣ����Ƶ�T�䣨0��0����
�����ڡ�O�ķ��Ƶ���ڣ����Ƶ�T�䣨0��0����
����OP��2r=2���ó�OP2��4����P��x����x+2�����ɹ��ɶ����ó�OP2=x2+����x+2��2=2x2��4x+4��4���ⲻ��ʽ�ó�0��x��2���ٷֱ�x=2��0������鼴�ɣ�
��2������y=��![]() x+2
x+2![]() �����A��6��0����B��0��2
�����A��6��0����B��0��2![]() ������
������![]() =
=![]() ����OBA=60�㣬��OAB=30�㣮����C��x��0��������������������ۣ���C��OA�ϣ���C��A���Ҳ�.
����OBA=60�㣬��OAB=30�㣮����C��x��0��������������������ۣ���C��OA�ϣ���C��A���Ҳ�.
���⿼����Բ���ۺ�Ӧ�ã��漰֪ʶ���й��ɶ����������ԳƵ㡱�Ķ�����Ӧ��.

����Ŀ��Ϊ��ӭ��֣���еڶ��조�г�����������У����������ijѧУ��֯��һ������֪ʶ������ÿ��ѡ25��ͬѧ�μӱ������ɼ��ֱ�ΪA��B��C��D�ĸ��ȼ���������Ӧ�ȼ��÷����μ�Ϊ100�֡�90�֡�80�֡�70�֣�ѧУ�����꼶һ��Ͷ���ijɼ����������Ƴ�ͳ��ͼ����ͼ��ʾ��
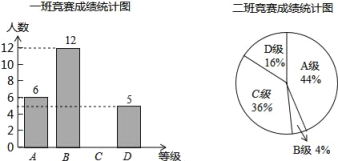
��1����һ�ྺ���ɼ�ͳ��ͼ����������
��2��д���±���a��b��c��ֵ��
ƽ�������֣� | ��λ�����֣� | �������֣� | ���� | |
һ�� | a | b | 90 | 106.24 |
���� | 87.6 | 80 | c | 138.24 |
��3�����ݣ�2���Ľ�����������ξ����ɼ��Ľ�����з�����
����Ŀ��LED�ƾ��л������ܡ�Ͷ�䷶Χ����Ƶ����ʹ�������ϳ����ص㣬���ճ������У����Ǹ�������LED�Ƶ�ʹ�ã�ijУ��ѧ��ȤС��Ϊ�˽�LED��������ͨ�׳���ݵ�����������������г����飺ij�̳�����һ��30�ߵ�LED���ݺ���ͨ�׳���ݽ������ۣ�������������±���
LED���� | ��ͨ�׳���� | |
���ۣ�Ԫ�� | 45 | 25 |
��ۣ�Ԫ�� | 60 | 30 |

��1�����̳�������LED��������ͨ�׳���ݹ�300����LED���ݰ���۽������ۣ�����ͨ�׳���ݴ�������ۣ����������������ݺ���Ի���3200Ԫ������̳�����LED��������ͨ�׳���ݵ������ֱ�Ϊ���ٸ���
��2�����ڴ����ڼ��������ܿ콫���ֵ��������꣬�����̳��ƻ��ٴι������ֵ���120�����ڲ����۵�����£�������ν�������������������ʱ��������Ҳ����������۵�30%���������ʱ�������ݵ�������Ϊ����Ԫ��