Question

【题目】在直角坐标系中，设x轴为直线l，函数y=﹣ x，y= x的图象分别是直线l1 ， l2 ， 圆P（以点P为圆心，1为半径）与直线l，l1 ， l2中的两条相切．例如（ ，1）是其中一个圆P的圆心坐标．
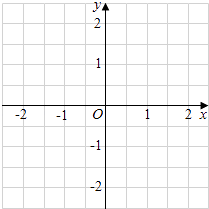
（1）写出其余满足条件的圆P的圆心坐标；
（2）在图中标出所有圆心，并用线段依次连接各圆心，求所得几何图形的周长．

Answer 1

【答案】
（1）解：①若圆P与直线l和l2都相切，

当点P在第四象限时，

过点P作PH⊥x轴，垂足为H，连接OP，如图1所示．

设y= x的图象与x轴的夹角为α．

当x=1时，y= ．

∴tanα= ．

∴α=60°．

∴由切线长定理得：∠POH= ×（180°﹣60°）=60°．

∵PH=1，

∴tan∠POH= = = ．

∴OH= ．

∴点P的坐标为（ ，﹣1）．

同理可得：

当点P在第二象限时，点P的坐标为（﹣ ，1）；

当点P在第三象限时，点P的坐标为（﹣ ，﹣1）；

②若圆P与直线l和l1都相切，如图2所示．

同理可得：当点P在第一象限时，点P的坐标为（ ，1）；

当点P在第二象限时，点P的坐标为（﹣ ，1）；

当点P在第三象限时，点P的坐标为（﹣ ，﹣1）；

当点P在第四象限时，点P的坐标为（ ，﹣1）．

③若圆P与直线l1和l2都相切，如图3所示．

同理可得：

当点P在x轴的正半轴上时，点P的坐标为（ ，0）；

当点P在x轴的负半轴上时，点P的坐标为（﹣ ，0）；

当点P在y轴的正半轴上时，点P的坐标为（0，2）；

当点P在y轴的负半轴上时，点P的坐标为（0，﹣2）．

综上所述：其余满足条件的圆P的圆心坐标有：

（ ，﹣1）、（﹣ ，1）、（﹣ ，﹣1）、

（ ，1）、（﹣ ，1）、（﹣ ，﹣1）、（ ，﹣1）、

（ ，0）、（﹣ ，0）、（0，2）、（0，﹣2）

（2）解：用线段依次连接各圆心，所得几何图形，如图4所示．

由图可知：该几何图形既轴对称图形，又是中心对称图形，

由对称性可得：该几何图形的所有的边都相等．

∴该图形的周长=12×（ ﹣ ）=8 ．

【解析】（1）对圆P与直线l和l2都相切、圆P与直线l和l1都相切、圆P与直线l1和l2都相切三种情况分别考虑，利用切线长定理和特殊角的三角函数值即可求出点P的坐标．（2）由图可知：该几何图形既轴对称图形，又是中心对称图形，它的所有的边都相等．只需求出其中的一条边就可以求出它的周长．
【考点精析】利用切线长定理和轴对称图形对题目进行判断即可得到答案，需要熟知从圆外一点引圆的两条切线，它们的切线长相等圆心和这一点的连线平分两条切线的夹角；两个完全一样的图形关于某条直线对折，如果两边能够完全重合，我们就说这两个图形成轴对称，这条直线就对称轴．