题目内容
【题目】在ABCD中,过点D作DE⊥AB于点E,点F 在边CD上,DF=BE,连接AF,BF.
(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
【答案】
(1)
证明:∵四边形ABCD是平行四边形,
∴AB∥CD.
∵BE∥DF,BE=DF,
∴四边形BFDE是平行四边形.
∵DE⊥AB,
∴∠DEB=90°,
∴四边形BFDE是矩形;
(2)
解:∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠DFA=∠FAB.
在Rt△BCF中,由勾股定理,得
BC=![]() =
=![]() =5,
=5,
∴AD=BC=DF=5,
∴∠DAF=∠DFA,
∴∠DAF=∠FAB,
即AF平分∠DAB.
【解析】(1)根据平行四边形的性质,可得AB与CD的关系,根据平行四边形的判定,可得BFDE是平行四边形,再根据矩形的判定,可得答案;
(2)根据平行线的性质,可得∠DFA=∠FAB,根据等腰三角形的判定与性质,可得∠DAF=∠DFA,根据角平分线的判定,可得答案.
此题综合考查了平行四边形的判定与性质,矩形的判定以及等腰三角形和角平分线的性质等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某校为了了解学生孝敬父母的情况(选项:A.为父母洗一次脚;B.帮父母做一次家务;C.给父母买一件礼物;D.其它),在全校范围内随机抽取了若干名学生进行调查,得到如图表(部分信息未给出):学生孝敬父母情况统计表:
选项 | 频数 | 频率 |
A | m | 0.15 |
B | 60 | p |
C | n | 0.4 |
D | 48 | 0.2 |
根据以上信息解答下列问题: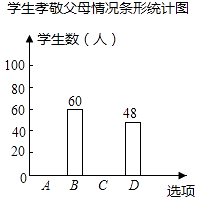
(1)这次被调查的学生有多少人?
(2)求表中m,n,p的值,并补全条形统计图.
(3)该校有1600名学生,估计该校全体学生中选择B选项的有多少人?