题目内容
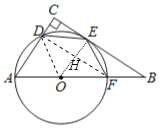
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 、
、![]() 、
、![]() 分别在
分别在![]() 、
、![]() 、
、![]() 边上,以
边上,以![]() 为直径⊙
为直径⊙![]() 的恰好经过
的恰好经过![]() 、
、![]() ,且
,且![]()
(1)求证:![]() 为⊙
为⊙![]() 的切线;
的切线;
(2)若![]() ,求
,求![]() 的度数;
的度数;
(3)若![]() ,
,![]() ,求⊙
,求⊙![]() 的半径及线段
的半径及线段![]() 的长
的长

【答案】(1)见解析;(2)65°;(3)![]()
【解析】
(1)证明:连接OD、OE、DF,如图,利用圆周角定理得∠ADF=90°,则DF∥BC,再证明OE⊥DF,则OE⊥BC,然后根据切线的判定定理得到结论;
(2)利用互余得到∠BOE=50°,则利用等腰三角形和三角形内角和计算出∠OFE=65°,然后根据圆内接四边形的性质可得到∠CDE的度数;
(3)利用四边形CDHE为矩形得到HE=CD=2,DH=CE=4,设⊙O的半径为r,则OH=OEHE=r2,OD=r,则利用勾股定理得到(r2)2+42=r2,解方程得到r=5,再证明△OHF∽△OEB,然后利用相似比可计算出BE.
解:(1)证明:连接OD、OE、DF,如图,
∵AF为直径,
∴∠ADF=90°,
而∠C=90°,
∴DF∥BC,
∵DE=EF,
∴![]()
∴OE⊥DF,
∴OE⊥BC,
∴BC为⊙O的切线;
(2)∵∠OEB=90°,∠B=40°,
∴∠BOE=90°﹣40°=50°,
∴∠OFE=![]() (180°﹣50°)=65°,
(180°﹣50°)=65°,
∴∠CDE=∠AFE=65°;
(3)解:∵∠C=∠OEC=90°
又OE⊥DF,
∴∠EHD=90°
∴四边形CDHE为矩形,
∴HE=CD=2,DH=CE=4,
设⊙O的半径为r,则OH=OE﹣HE=r﹣2,OD=r,
在Rt△OHD中,(r﹣2)2+42=r2,解得r=5,
∵OH⊥DF,
∴HF=DH=4,
∵HF∥BE,
∴△OHF∽△OEB,
∴HF:BE=OH:OE,即4:BE=3:5,
∴BE=![]() .
.

练习册系列答案
相关题目