题目内容
【题目】已知抛物线y=x2﹣mx+n经过点A(3,0).
(1)当m+n=﹣1时,求该抛物线的解析式和顶点坐标;
(2)当B点坐标为(0,﹣3)时,若抛物线y=x2﹣mx+n图象的顶点在直线AB上,求m、n的值;
(3)①设m=﹣2,当0≤x≤3时,求抛物线y=x2﹣mx+n的最小值;
②若当0≤x≤3时,二次函数y=x2﹣mx+n的最小值为﹣4,求m、n的值.
【答案】(1)y=x2﹣2x﹣3,顶点坐标为(1,﹣4);(2)![]() 或
或![]() ;(3)①-15;②m=2,n=﹣3.
;(3)①-15;②m=2,n=﹣3.
【解析】
(1)将点A(3,0)代入解析式,得9﹣3m+n=0,与m+n=1组成方程组,解方程组求得m、n即可;
(2)先表示出二次函数y=x2﹣mx+n图象的顶点,利用直线AB列出式子,再与点A在二次函数上得到的式子组成方程组求得m,n的值,
(3)①易求抛物线解析式为y=x2+2x﹣15.根据抛物线的对称性和增减性来求二次函数y=x2﹣mx+n的最小值;
②本题要分三种情况:当对称轴![]() 时;当对称轴
时;当对称轴![]() 时;当对称轴
时;当对称轴![]() 时,结合二次函数y=x2﹣mx+n的图象经过点A得出式子9﹣3m+n=0,求出m,n但一定要验证是否符合题意.
时,结合二次函数y=x2﹣mx+n的图象经过点A得出式子9﹣3m+n=0,求出m,n但一定要验证是否符合题意.
解:(1)将点A(3,0)代入y=x2﹣mx+n中,得9﹣3m+n=0,
又∵m+n=﹣1,
∴![]() ,解得
,解得![]() ,
,
∴抛物线的解析式为y=x2﹣2x﹣3,
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴顶点坐标为(1,﹣4).
(2)二次函数y=x2﹣mx+n图象的顶点坐标为![]() ,
,
设直线AB的解析式为y=kx+b,将A(3,0),B(0,﹣3)代入得![]() ,
,
解得![]()
∴直线AB的解析式为y=x﹣3,
∵抛物线顶点![]() 在直线AB上,
在直线AB上,
∴得![]() ,
,
又∵二次函数y=x2﹣mx+n的图象经过点A(3,0),
∴9﹣3m+n=0,
∴联立方程组得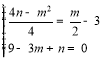 ,解得
,解得![]() 或
或![]() ;
;
(3)①∵二次函数y=x2﹣mx+n的图象经过点A(3,0),
∴9﹣3m+n=0,
当m=﹣2时,解得n=﹣15,
∴二次函数的解析式为y=x2+2x﹣15,
∵对称轴x=﹣1在0≤x≤3的左侧,且二次函数的图象开口向上,
∴x=0时,y取最小值,最小值是﹣15.
∴当0≤x≤3时,二次函数y=x2﹣mx+n的最小值为﹣15;
②二次函数y=x2﹣mx+n图象的对称轴为直线x=![]() ,顶点坐标为
,顶点坐标为![]() ,
,
ⅰ)当对称轴![]() ≥3时,即m≥6时,在0≤x≤3中,二次函数y=x2﹣mx+n的最小值的最小值为0,此种情况不合题意;
≥3时,即m≥6时,在0≤x≤3中,二次函数y=x2﹣mx+n的最小值的最小值为0,此种情况不合题意;
ⅱ)当对称轴0<![]() <3时,即0<m<6时,
<3时,即0<m<6时,
 解得
解得![]() 或
或![]() (舍去)
(舍去)
∴m=2,n=﹣3;
ⅲ)当对称轴![]() ≤0时,即m≤0时,
≤0时,即m≤0时,
![]() 解得
解得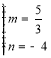 (舍去),
(舍去),
综上所述当0≤x≤3时,二次函数y=x2﹣mx+n的最小值为﹣4时,m=2,n=﹣3.

【题目】阅读对学生的成长有着深远的影响,某中学为了解学生每周课余阅读的时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表.
组别 | 时间(小时) | 频数(人数) | 频率 |
A | 0≤t≤0.5 | 6 | 0.15 |
B | 0.5≤t≤1 | a | 0.3 |
C | 1≤t≤1.5 | 10 | 0.25 |
D | 1.5≤t≤2 | 8 | b |
E | 2≤t≤2.5 | 4 | 0.1 |
合计 | 1 |
请根据图表中的信息,解答下列问题:
(1)表中的a= ,b= ,中位数落在 组,将频数分布直方图补全;
(2)估计该校2000名学生中,每周课余阅读时间不足0.5小时的学生大约有多少名?
(3)E组的4人中,有1名男生和3名女生,该校计划在E组学生中随机选出两人向全校同学作读书心得报告,请用画树状图或列表法求抽取的两名学生刚好是1名男生和1名女生的概率.