题目内容
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,E是边
,E是边![]() 的中点,点P在边
的中点,点P在边![]() 上,设
上,设![]() ,若以点D为圆心,
,若以点D为圆心,![]() 为半径的
为半径的![]() 与线段
与线段![]() 只有一个公共点,则所有满足条件的x的取值范围是______.
只有一个公共点,则所有满足条件的x的取值范围是______.

【答案】x=![]() 或
或![]()
【解析】
根据题意,当![]() 与AE相切时,由相似三角形的性质,可得:
与AE相切时,由相似三角形的性质,可得:![]() ,从而求出x的值,当
,从而求出x的值,当![]() 过点E时,x=PD=DE,当
过点E时,x=PD=DE,当![]() 过点A时,x=PD=AD,进而求出x满足的条件.
过点A时,x=PD=AD,进而求出x满足的条件.
如图1,当![]() 与AE相切时,设切点为G,连接DG,
与AE相切时,设切点为G,连接DG,
∵![]() ,
,
∴DG=DP=x,
∵∠DAG=∠AEB,∠AGD=∠B=90°,
∴AGD~EBA,
∴![]() ,
,
∴![]() ,解得:x=
,解得:x=![]() ,
,
如图2,当![]() 过点E时,
过点E时,![]() 与线段AE有两个公共点,连接DE,此时,PD=DE=5,
与线段AE有两个公共点,连接DE,此时,PD=DE=5,
∴x=PD=5
如图3,当![]() 过点A时,
过点A时,![]() 与线段AE有1个公共点,此时,PD=AD=6,
与线段AE有1个公共点,此时,PD=AD=6,
∴x=PD=6,
综上所述:当![]() 与线段AE只有一个公共点时,x满足的条件是:x=
与线段AE只有一个公共点时,x满足的条件是:x=![]() 或
或![]() ;
;
故答案是:x=![]() 或
或![]() .
.
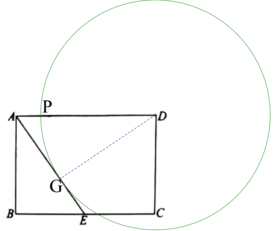

图1 图2
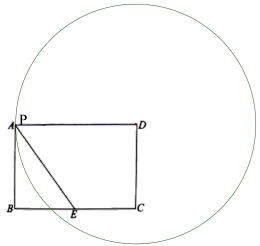
图3

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
【题目】阅读对学生的成长有着深远的影响,某中学为了解学生每周课余阅读的时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表.
组别 | 时间(小时) | 频数(人数) | 频率 |
A | 0≤t≤0.5 | 6 | 0.15 |
B | 0.5≤t≤1 | a | 0.3 |
C | 1≤t≤1.5 | 10 | 0.25 |
D | 1.5≤t≤2 | 8 | b |
E | 2≤t≤2.5 | 4 | 0.1 |
合计 | 1 |
请根据图表中的信息,解答下列问题:
(1)表中的a= ,b= ,中位数落在 组,将频数分布直方图补全;
(2)估计该校2000名学生中,每周课余阅读时间不足0.5小时的学生大约有多少名?
(3)E组的4人中,有1名男生和3名女生,该校计划在E组学生中随机选出两人向全校同学作读书心得报告,请用画树状图或列表法求抽取的两名学生刚好是1名男生和1名女生的概率.