Question

【题目】已知等边△ABC，点D为BC上一点，连接AD.

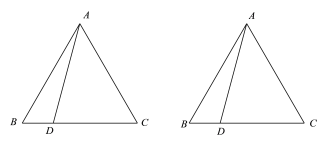
图1 图2

（1）若点E是AC上一点，且CE＝BD，连接BE，BE与AD的交点为点P，在图（1）中根据题意补全图形，直接写出∠APE的大小；

（2）将AD绕点A逆时针旋转120°，得到AF，连接BF交AC于点Q，在图（2）中根据题意补全图形，用等式表示线段AQ和CD的数量关系，并证明.

Answer 1

【答案】（1）补全图形见解析. ∠APE=60°；（2）补全图形见解析.，证明见解析.

【解析】

（1）根据题意，按照要求补全图形即可；

（2）先补全图形，然后首先证明△ABD≌△BEC得出∠BAD=∠CBE，之后通过一系列证明得出△AQF≌△EQB，最后进一步从而得出即可.

（1）补全图形如下，其中 ∠APE=60°，

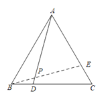
（2）补全图形.

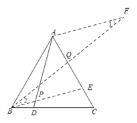
证明：在△ABD和△BEC中，

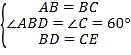
∴△ABD≌△BEC（SAS）

∴∠BAD=∠CBE.

∵∠APE是△ABP的一个外角，

∴∠APE=∠BAD+∠ABP=∠CBE+∠ABP=∠ABC=60°.

∵AF是由AD绕点A逆时针旋转120°得到，

∴AF=AD，∠DAF=120°.

∵∠APE=60°，

∴∠APE+∠DAP=180°.

∴AF∥BE

∴∠1=∠2

∵△ABD≌△BEC，

∴AD=BE.

∴AF=BE.

在△AQF和△EQB中，

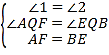
∴△AQF≌△EQB（AAS）

∴AQ=QE

∴

∵AE=AC－CE，CD=BC－BD，

且AE=BC，CD=BD.

∴AE=CD..

∴