题目内容
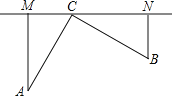
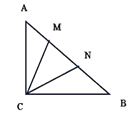
【题目】如图,△ABC中,∠ACB=90°,AC=AN,BC=BM,则∠MCN=( )
A. 30°B. 45°C. 60°D. 55°
【答案】B
【解析】
设∠BMC=x,∠ANC=y.由BC=BM,根据等边对等角得出∠BCM=∠BMC=x,利用三角形内角和定理得出∠B=180°-2x.同理得到∠ACN=∠ANC=y,∠A=180°-2y.根据直角三角形两锐角互余得出∠A+∠B=90°,那么x+y=135°,即∠BCM+∠ACN=135°,进而求出∠MCN=∠BCM+∠ACN-∠ACB=45°.
设∠BMC=x,∠ANC=y.
∵BC=BM,
∴∠BCM=∠BMC=x,∠B=180°-2x.
∵AC=AN,
∴∠ACN=∠ANC=y,∠A=180°-2y.
∵△ABC为直角三角形,∠ACB=90°,
∴∠A+∠B=90°,
∴180°-2y+180°-2x=90°,
∴x+y=135°,
∴∠BCM+∠ACN=135°,
∴∠MCN=∠BCM+∠ACN-∠ACB=135°-90°=45°.
故选B.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目