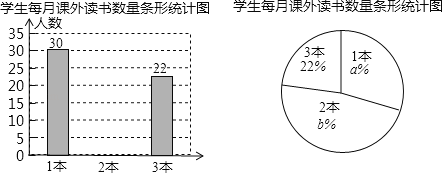
题目内容
【题目】如图,在△ABC中,AC=AB,∠BAC=90°,D是AC边上一点,连接BD,AF⊥BD于点F,点E在BF上,连接AE,∠EAF=45°,连接CE,AK⊥CE于点K,交DE于点H,∠DEC=30°,HF=![]() ,则EC=______
,则EC=______
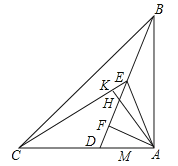
【答案】6
【解析】
延长AF交CE于P,证得△ABH≌△APC得出AH=CP,证得△AHF≌△EPF得出AH=EP,得出EC=2AH,解30°的直角三角形AFH求得AH,即可求得EC的长.
如图,延长AF交CE于P,
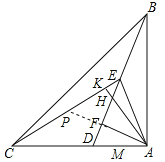
∵∠ABH+∠ADB=90°,∠PAC+∠ADB=90°,
∴∠ABH=∠PAC,
∵AK⊥CE,AF⊥BD,∠EHK=∠AHF,
∴∠HEK=∠FAH,
∵∠FAH+∠AHF=90°,∠HEK+∠EPF=90°,
∴∠AHF=∠EPF,
∴∠AHB=∠APC,
在△ABH与△APC中,
 ,
,
∴△ABH≌△APC(ASA),
∴AH=CP,
在△AHF与△EPF中,
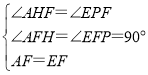 ,
,
∴△AHF≌△EPF(AAS),
∴AH=EP,∠CED=∠HAF,
∴EC=2AH,
∵∠DEC=30°,
∴∠HAF=30°,
∴AH=2FH=2×![]() =3,
=3,
∴EC=2AH=6.

练习册系列答案
相关题目