题目内容
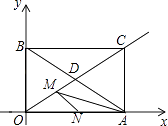
【题目】如图1，在正方形ABCD中，P是对角线BD上的点，点E在AB上，且PA=PE．
（1）求证：PC=PE；
（2）求∠CPE的度数；
（3）如图2，把正方形ABCD改为菱形ABCD，其他条件不变，试探究∠CPE与∠ABC之间的数量关系，并说明理由．
【答案】
（1）证明：在正方形ABCD中，AB=BC，
∠ABP=∠CBP=45°，
在△ABP和△CBP中，
，
∴△ABP≌△CBP（SAS），
∴PA=PC，
∵PA=PE，
∴PC=PE；
（2）解：由（1）知，△ABP≌△CBP，
∴∠BAP=∠BCP，
∵PA=PE，
∴∠PAE=∠PEA，
∴∠CPB=∠AEP，
∵∠AEP+∠PEB=180°，
∴∠PEB+∠PCB=180°，
∴∠ABC+∠EPC=180°，
∵∠ABC=90°，
∴∠EPC=90°
（3）∠ABC+∠EPC=180°，
理由：解：在菱形ABCD中，AB=BC，∠ABP=∠CBP=60°，
在△ABP和△CBP中，
，
∴△ABP≌△CBP（SAS），
∴∠BAP=∠BCP，
∵PA=PE，
∴∠DAP=∠DCP，
∴∠PAE=∠PEA，
∴∠CPB=∠AEP，
∵∠AEP+∠PEB=180°，
∴∠PEB+∠PCB=180°，
∴∠ABC+∠EPC=180°
【解析】（1）根据正方形的性质，四边相等，四个角为90°，且对角线平分对角，即可证出△ABP≌△CBP（SAS），得PA＝PC，由于PA＝PE，得PC＝PE
（２）利用全等的性质，由△ABP≌△CBP，得∠BAP=∠BCP，进而得∠DAP=∠DCP,由PA＝PE，∠PAE=∠PEA，最后通过同角的补角的关系得到∠ABC+∠EPC=180°，以及四边形的内角和为360°，∠CPF=∠EDF=90°最后得出结论
（3）此题为一二题的变式题，借助(1)和(2)证明方法第三题易证，且菱形和正方形除了每个角不是直角以为，其他的性质都是共性，即可证出△ABP≌△CBP（SAS），得到∠BAP=∠BCP，然后根据等腰三角形的等边对等角得∠DAP=∠DCP，最后再通过同角的补角关系和四边形的内角和为360°即可得出结论。
【考点精析】关于本题考查的菱形的性质和正方形的性质，需要了解菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半；正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能得出正确答案．
