题目内容
【题目】如图，矩形AOBC，点A、B分别在x、y轴上，对角线AB、OC交于点D，点C（ 
，1），点M是射线OC上一动点．
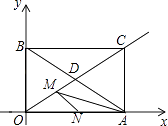
（1）求证：△ACD是等边三角形；
（2）若△OAM是等腰三角形，求点M的坐标；
（3）若N是OA上的动点，则MA+MN是否存在最小值？若存在，请求出这个最小值；若不存在，请说明理由．
【答案】
（1）证明：∵C（ 
，1），
∴AC=1，OA= ，
∴OC=2，
∴∠COA=30°，∠OCA=60°，
∵矩形AOBC，
∴AD＝CD=OD
且∠OCA=60°
∴△ACD是等边三角形
（2）解：△OAM是等腰三角形，
当OM=MA时，此时点M与点D重合，
∵C（ ，1），点D为OC中点，
∴M（ 
， 
）．
当OM1=OA时，做M1E⊥OA，垂足为E，如下图：
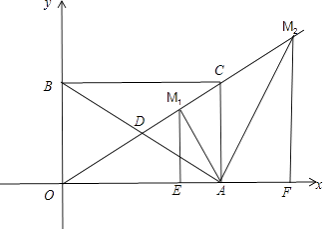
∴OM1=OA= ，
由（1）知∠M1OA=30°，
∴M1E= ，OE= 
，
∴M1（ ， ）．
当OA=OM2时，做M2F⊥OA，垂足为F，如上图：
AM2= ，
由（1）知∠COA=∠AM2O=30°，
∴∠M2AF=60°，
∴AF= ，M2F= ，
M2（ 
， ）．
综上所述：点M坐标为M（ ， ）、（ ， ）、（ ， ）
（3）解：存在，做点A关于直线OC对称点为G，如下图：
则AG⊥OC，且∠GOA=60°OG=OA= ，
∴ON= ，GN= ，
∵点A、G关于直线OC对称，
∴MG=MA，
∴MA+MN=MG+MN，
∵N是OA上的动点，
∴当GN⊥x轴时，MA+MN最小，
∴存在MA+MN存在最小值，最小值为 ．
【解析】（1）利用点C(
3，1)，即可求出相应角度为30°，则∠OCA=60°，根据矩形的性质和直角三角形中斜边的中线等于斜边的一半，则得出了有两边相等，且有一个角是60°，即可证明三角形是等边三角形；
（2）此问结合了分类讨论的思想，由等腰三角形性质，对三角形OAM三边关系进行讨论，分别求出三种情况讨论，三种情况都是转换不同的边为底边，另外两边相等，然后根据不同的情况求出点M的坐标即可；
（3）根据最短路径探究，做点A关于直线OC对称点，利用对称性可以求出最小值。
【考点精析】本题主要考查了含30度角的直角三角形和矩形的性质的相关知识点，需要掌握在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半；矩形的四个角都是直角，矩形的对角线相等才能正确解答此题．
