题目内容
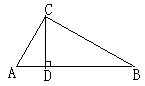
(本题9分)两个全等的直角三角形ABC和DEF重叠在一起,其中∠A=60°,AC="1." 固定△ABC不动,将△DEF进行如下操作:
(1)如图1,△DEF沿线段AB向右平移(即D点在线段AB内移动),连结DC、CF、FB,四边形CDBF的形状在不断的变化,但它的面积不变化,请求出其面积.

(2)如图2,当D点移到AB的中点时,请你猜想四边形CDBF的形状,并说明理由.

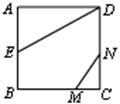
 (3)如图3,△DEF的D点固定在AB的中点,然后绕D点按顺时针方向旋转△DEF,使DF落在AB边上,此时F点恰好与B点重合,连结AE,请你求出sinAED的值.
(3)如图3,△DEF的D点固定在AB的中点,然后绕D点按顺时针方向旋转△DEF,使DF落在AB边上,此时F点恰好与B点重合,连结AE,请你求出sinAED的值.
(1)如图1,△DEF沿线段AB向右平移(即D点在线段AB内移动),连结DC、CF、FB,四边形CDBF的形状在不断的变化,但它的面积不变化,请求出其面积.

(2)如图2,当D点移到AB的中点时,请你猜想四边形CDBF的形状,并说明理由.

 (3)如图3,△DEF的D点固定在AB的中点,然后绕D点按顺时针方向旋转△DEF,使DF落在AB边上,此时F点恰好与B点重合,连结AE,请你求出sinAED的值.
(3)如图3,△DEF的D点固定在AB的中点,然后绕D点按顺时针方向旋转△DEF,使DF落在AB边上,此时F点恰好与B点重合,连结AE,请你求出sinAED的值.
(1)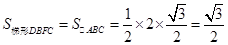 ;(2)四边形CDBF是菱形;
;(2)四边形CDBF是菱形;
(3) sinα=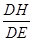 =
=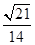 。
。
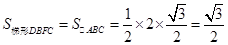 ;(2)四边形CDBF是菱形;
;(2)四边形CDBF是菱形;(3) sinα=
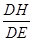 =
=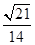 。
。此题主要考查了菱形的判定,综合运用直角三角形的性质和平移的性质进行分析计算,考查学生综合运用数学知识的能力.
(1)过点C作CG⊥AB于G
在Rt△ACG中 ∵∠A=60°
∴sin60°= ,得到结论。
,得到结论。
(2)根据直角三角形斜边上的中线等于斜边的一半和平移的性质,即可得到该四边形的四条边都相等,则它是一个菱形;
(3)在Rt△ABE中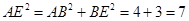
∴ 过点D作DH⊥AE 垂足为H
过点D作DH⊥AE 垂足为H
则△ADH∽△AEB 得到相似比求解得到。

(1)过点C作CG⊥AB于G
在Rt△ACG中 ∵∠A=60°
∴sin60°= ∴
∴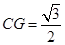 ……………1分
……………1分
在Rt△ABC中 ∠ACB=90°∠ABC=30°
∴AB=2 …………………………………………2分
∴ ………3分
………3分
(2)菱形………………………………………4分
∵D是AB的中点 ∴AD=DB=CF=1
在Rt△ABC中,CD是斜边中线 ∴CD=1……5分
同理 BF=1 ∴CD=DB=BF=CF
∴四边形CDBF是菱形…………………………6分
(3)在Rt△ABE中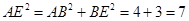
∴ ……………………………7分
……………………………7分
过点D作DH⊥AE 垂足为H
则△ADH∽△AEB ∴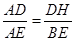
即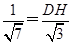 ∴ DH=
∴ DH=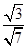 ……8分
……8分
在Rt△DHE中
sinα=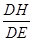 =…=
=…=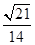 …………………9分
…………………9分
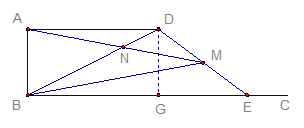
(1)过点C作CG⊥AB于G
在Rt△ACG中 ∵∠A=60°
∴sin60°=
 ,得到结论。
,得到结论。(2)根据直角三角形斜边上的中线等于斜边的一半和平移的性质,即可得到该四边形的四条边都相等,则它是一个菱形;
(3)在Rt△ABE中
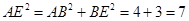
∴
 过点D作DH⊥AE 垂足为H
过点D作DH⊥AE 垂足为H则△ADH∽△AEB 得到相似比求解得到。

(1)过点C作CG⊥AB于G
在Rt△ACG中 ∵∠A=60°
∴sin60°=
 ∴
∴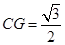 ……………1分
……………1分在Rt△ABC中 ∠ACB=90°∠ABC=30°
∴AB=2 …………………………………………2分
∴
 ………3分
………3分(2)菱形………………………………………4分
∵D是AB的中点 ∴AD=DB=CF=1
在Rt△ABC中,CD是斜边中线 ∴CD=1……5分
同理 BF=1 ∴CD=DB=BF=CF
∴四边形CDBF是菱形…………………………6分
(3)在Rt△ABE中
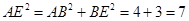
∴
 ……………………………7分
……………………………7分过点D作DH⊥AE 垂足为H
则△ADH∽△AEB ∴
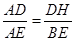
即
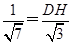 ∴ DH=
∴ DH=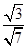 ……8分
……8分在Rt△DHE中
sinα=
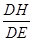 =…=
=…=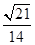 …………………9分
…………………9分

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
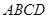 中,过
中,过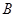 点作
点作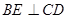 ,垂足为
,垂足为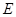 ,连结
,连结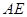 ,
,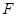 为
为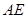 上一点,且
上一点,且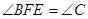 。
。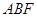 ∽△
∽△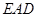 ;
;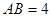 ,
,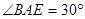 ,求
,求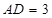 ,求
,求 的长.
的长.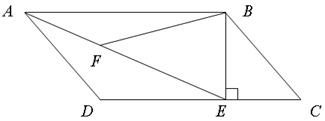

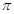 m2的圆.已知圆桌的高度为1m,圆桌面的半径为0.5m,试求吊灯距圆桌面的距离.
m2的圆.已知圆桌的高度为1m,圆桌面的半径为0.5m,试求吊灯距圆桌面的距离.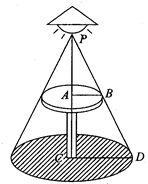
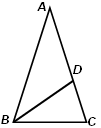
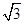 ,则△ADC的面积与△CDB的面积的比为( )
,则△ADC的面积与△CDB的面积的比为( )