题目内容
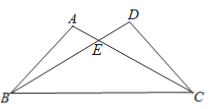
【题目】如图,直线CB∥OA,∠C=∠A=112°,E,F在CB上,且满足∠FOB=∠AOB,DE平分∠COF.
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.

【答案】(1)∠EOB=34°; (2)∠OBC:∠OFC=1:2,是定值;(3)存在某种情况,使∠OEC=∠OBA,此时∠OEC=∠OBA=51°.
【解析】
(1)根据两直线平行,同旁内角互补求出∠AOC,再根据角平分线的定义求出∠EOB=![]() ∠AOC,代入数据即可得解;
∠AOC,代入数据即可得解;
(2)根据两直线平行,内错角相等可得∠AOB=∠OBC,从而得到∠OBC=∠FOB,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠OFC=2∠OBC,从而得解;
(3)根据三角形内角和定理求出∠COE=∠AOB,从而得到OB、OE、OF是∠AOC的四等分线,再利用三角形内角和定理列式计算即可得解.
(1)∵CB∥OA,
∴∠AOC=180°-∠C=180°-112°=68°,
∵OE平分∠COF,
∴∠COE=∠EOF,
∵∠FOB=∠AOB,
∴∠EOB=∠EOF+∠FOB=![]() ∠AOC=
∠AOC=![]() ×68°=34°;
×68°=34°;
(2)∠OBC:∠OFC的值不变.
∵CB∥OA,
∴∠AOB=∠OBC,
∵∠FOB=∠AOB,
∴∠FOB=∠OBC,
∴∠OFC=∠FOB+∠OBC=2∠OBC,
∴∠OBC:∠OFC=1:2,是定值;
(3)在△COE和△AOB中,
∵∠OEC=∠OBA,∠C=∠OAB,
∴∠COE=∠AOB,
∴OB、OE、OF是∠AOC的四等分线,
∴∠COE=![]() ∠AOC=
∠AOC=![]() ×68°=17°,
×68°=17°,
∴∠OEC=180°-∠C-∠COE=180°-112°-17°=51°,
故存在某种情况,使∠OEC=∠OBA,此时∠OEC=∠OBA=51°.

【题目】某公交公司有A,B型两种客车,它们的载客量和租金如下表:
A | B | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 400 | 280 |
某中学根据实际情况,计划租用A,B型客车共5辆,同时送七年级师生到基地校参加社会实践活动.设租用A型客车x辆,根据要求回答下列问题:
(1)用含x的式子填写下表:
车辆数(辆) | 载客量 | 租金(元) | |
A | x | 45x | 400x |
B | 5-x |
(2)若要保证租车费用不超过1900元,求x的最大值.