题目内容
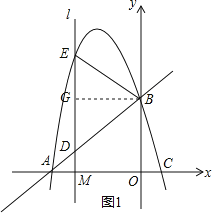
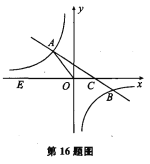
【题目】(2017贵州省遵义市)如图,抛物线![]() (a<0,a、b为常数)与x轴交于A、C两点,与y轴交于B点,直线AB的函数关系式为
(a<0,a、b为常数)与x轴交于A、C两点,与y轴交于B点,直线AB的函数关系式为![]() .
.
(1)求该抛物线的函数关系式与C点坐标;
(2)已知点M(m,0)是线段OA上的一个动点,过点M作x轴的垂线l分别与直线AB和抛物线交于D、E两点,当m为何值时,△BDE恰好是以DE为底边的等腰三角形?
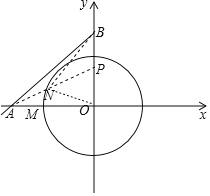
(3)在(2)问条件下,当△BDE恰好是以DE为底边的等腰三角形时,动点M相应位置记为点M′,将OM′绕原点O顺时针旋转得到ON(旋转角在0°到90°之间);
①探究:线段OB上是否存在定点P(P不与O、B重合),无论ON如何旋转,![]() 始终保持不变,若存在,试求出P点坐标;若不存在,请说明理由;
始终保持不变,若存在,试求出P点坐标;若不存在,请说明理由;
②试求出此旋转过程中,(NA+![]() NB)的最小值.
NB)的最小值.

【答案】(1)![]() ,C(1,0);(2)m=﹣4;(3)①存在,P(0,3);②
,C(1,0);(2)m=﹣4;(3)①存在,P(0,3);②![]() .
.
【解析】试题分析:(1)根据已知条件得到B,A的坐标,解方程组得到抛物线的函数关系式,令y=0,于是得到C的坐标;
(2)由点M(m,0),过点M作x轴的垂线l分别与直线AB和抛物线交于D、E两点,得到D(m,![]() ),当DE为底时,作BG⊥DE于G,根据等腰三角形的性质得到EG=GD=
),当DE为底时,作BG⊥DE于G,根据等腰三角形的性质得到EG=GD=![]() ED,GM=OB=
ED,GM=OB=![]() ,列方程即可得到结论;
,列方程即可得到结论;
(3)①根据已知条件得到ON=OM′=4,OB=![]() ,由∠NOP=∠BON,特殊的当△NOP∽△BON时,根据相似三角形的性质得到
,由∠NOP=∠BON,特殊的当△NOP∽△BON时,根据相似三角形的性质得到![]() ,于是得到结论;
,于是得到结论;
②根据题意得到N在以O为圆心,4为半径的半圆上,由①知,![]() ,得到NP=
,得到NP=![]() NB,于是得到(NA+
NB,于是得到(NA+![]() NB)的最小值=NA+NP,此时N,A,P三点共线,根据勾股定理得到结论.
NB)的最小值=NA+NP,此时N,A,P三点共线,根据勾股定理得到结论.
试题解析:(1)在![]() 中,令x=0,则y=
中,令x=0,则y=![]() ,令y=0,则x=﹣6,
,令y=0,则x=﹣6,
∴B(0,![]() ),A(﹣6,0),
),A(﹣6,0),
把B(0,![]() ),A(﹣6,0)代入
),A(﹣6,0)代入![]() 得:
得: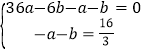 ,
,
∴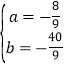 ,
,
∴抛物线的函数关系式为:![]() ,
,
令y=0,则![]() =0,
=0,
∴x1=﹣6,x2=1,
∴C(1,0);
(2)∵点M(m,0),过点M作x轴的垂线l分别与直线AB和抛物线交于D、E两点,
∴D(m,![]() ),
),
当DE为底时,作BG⊥DE于G,则EG=GD=![]() ED,GM=OB=
ED,GM=OB=![]() ,
,
∴![]() =
=![]() ,解得:m1=﹣4,m2=9(不合题意,舍去),
,解得:m1=﹣4,m2=9(不合题意,舍去),
∴当m=﹣4时,△BDE恰好是以DE为底边的等腰三角形;
(3)①存在,
∵ON=OM′=4,OB=![]() ,
,
∵∠NOP=∠BON,
∴当△NOP∽△BON时,![]() ,
,
∴![]() 不变,即OP=
不变,即OP=![]() =3,
=3,
∴P(0,3);
②∵N在以O为圆心,4为半径的半圆上,由①知,![]() ,
,
∴NP=![]() NB,
NB,
∴(NA+![]() NB)的最小值=NA+NP,
NB)的最小值=NA+NP,
∴此时N,A,P三点共线,
∴(NA+![]() NB)的最小值=
NB)的最小值=![]() =
=![]() .
.