题目内容
【题目】将函数
的图象位于
轴下方的部分沿轴翻折至其上方后，所得的是新函数
的图象.若该新函数图象与直线
有两个交点，则
的取值范围为___________．
【答案】
或
【解析】
根据题意画出新函数的图像，当直线
与
(
)只有一个交点时，可得方程
有两个相等的实数根，进而可求得此时b的值，将此时的直线向上平移即可得到符合题意的直线；再将点（1，0）和点（
，0）分别代入直线函数关系式，可得到两个特殊的b的值，结合函数图像可得符合题意的b的取值范围即可．
解：
的图象如图所示：
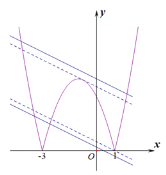
当直线与
()
只有一个交点时，
函数的图象与直线
有三个交点，
当直线与()只有一个交点，
此时方程有两个相等的实数根，
整理得
有两个相等的实数根，
，
解得
，
此时直线的解析式为：
，
若将此直线向上平移时该新函数图象与直线有两个交点，此时；
令中的y=0，
则
解得：
∴新函数的图象与x轴的交点坐标为（1，0），（3，0），
当直线经过点（1，0）时，
函数的图象与直线有三个交点，
将点（1，0）代入
得：
，
，
当直线经过点（，0）时，
函数的图象与直线有1个交点，
将点（，0）代入
得：
，
，
∴当该新函数图象与直线有两个交点时，；
综合可知：或．
故答案为：或．
励耘书业暑假衔接宁波出版社系列答案
【题目】某公司计划从甲、乙两种产品中选择一种生产并销售，每年产销
件．已知产销两种产品的有关信息如下表：
产品 | 每件售价（万元） | 每件成本（万元） | 每年其他费用（万元） | 每年最大产销量（件） |
甲 | 6 |
| 20 | 200 |
乙 | 30 | 20 |
| 80 |
其中
为常数，且
．
（1）若产销甲、乙两种产品的年利润分别为
万元、
万元，直接写出、与的函数关系式（写出自变量的取值范围）；
（2）分别求出产销两种产品的最大年利润；
（3）为获得最大年利润，该公司应该选择产销哪种产品？请说明理由．
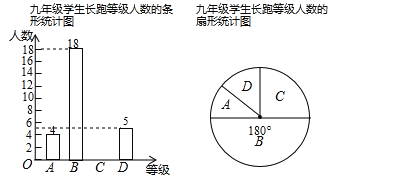
【题目】某学校七年级共有500名学生，为了解该年级学生的课外阅读情况，将从中随机抽取的40名学生一个学期的阅读量(阅读书籍的本数)作为样本，根据数据绘制了如下的表格和统计图：
等级 | 阅读量( | 频数 | 频率 |
E | x≤2 | 4 | 0.1 |
D | 2<x≤4 | 12 | 0.3 |
C | 4<x≤6 | a | 0.35 |
B | 6<x≤8 | c | b |
A | x>8 | 4 | 0.1 |
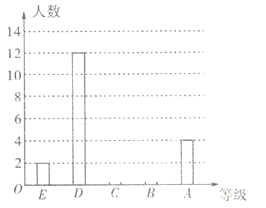
根据上面提供的信息，回答下列问题：
(1)统计表中的
，
；并补全条形统计图；
(2)根据抽样调查结果，请估计该校七年级学生一学期的阅读量为“
等”的有多少人?
(3)样本中阅读量为“等”的4名学生中有2名男生和2名女生，现从中随机挑选2名同学参加区里举行的“语文学科素养展示”活动，请用树状图法或列表法求出恰好选中“1男1女”的概率．
