题目内容
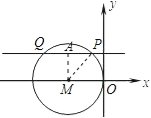
【题目】如图,在平面直角坐标系中,⊙M与y轴相切于原点O,平行于x轴的直线交⊙M于P、Q两点,点P在点Q的右边,若P点的坐标为(-1,2),则Q点的坐标是

A. (-4,2) B. (-4.5,2) C. (-5,2) D. (-5.5,2 )
【答案】A
【解析】试题分析:因为⊙M与y轴相切于原点O,平行于x轴的直线交⊙M于P,Q两点,点P在点Q的右方,若点P的坐标是(﹣1,2),则点Q的坐纵标是2,设PQ=2x,作MA⊥PQ,利用垂径定理可求QA=PA=x,连接MP,则MP=MO=x+1,在Rt△AMP中,利用勾股定理即可求出x的值,从而求出Q的横坐标=﹣(2x+1).
解:∵⊙M与y轴相切于原点O,平行于x轴的直线交⊙M于P,Q两点,点P在点Q的右方,点P的坐标是(﹣1,2)
∴点Q的纵坐标是2
设PQ=2x,作MA⊥PQ,
利用垂径定理可知QA=PA=x,
连接MP,则MP=MO=x+1,
在Rt△AMP中,MA2+AP2=MP2
∴22+x2=(x+1)2∴x=1.5
∴PQ=3,Q的横坐标=﹣(1+3)=﹣4
∴Q(﹣4,2)
故选:A.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目