题目内容
【题目】为了解某次“小学生书法比赛”的成绩情况,随机抽取了30名学生的成绩进行统计,并将统计情况绘成如图所示的频数分布直方图,己知成绩x(单位:分)均满足“50≤x<100”,每组成绩包含最小值,不包含最大值.根据图中信息回答下列问题:
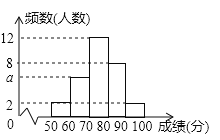
(1)图中a的值为_____;若要绘制该样本的扇形统计图,则成绩x在“70≤x<80”所对应扇形的圆心角度数为__________;
(2)此次比赛共有300名学生参加,若将“x≥80”的成绩记为“优秀”,则获得“优秀“的学生大约有多少人?
(3)在这些抽查的样本中,小明的成绩为92分,若从成绩在“50≤x<60”和“90≤x<100”的学生中任选2人,请用列表或画树状图的方法,求小明被选中的概率.
【答案】(1)6,144°;(2)100人;(3)见解析,![]() .
.
【解析】
(1)用总人数减去其他分组的人数即可求得60![]() x<70的人数a;用360乘以成绩在70≤x<80的人数所占比例可得;
x<70的人数a;用360乘以成绩在70≤x<80的人数所占比例可得;
(2)用总人数乘以样本中优秀人数所占比例即可得;
(3)先画出树状图展示所有12种等可能的结果数,再找出有C的结果数,然后根据概率公式求解.
解:(1)a=30-(2+12+8+2)=6;成绩在“70≤x<80所对应扇形的圆心角度数为360°×![]() =144°;故答案为:6,144;
=144°;故答案为:6,144;
(2)获得“优秀“的学生大约有300×![]() =100人,故答案为:100人;
=100人,故答案为:100人;
(3)50≤x<60的两名同学用A、B表示,90≤x<100的两名同学用C(小明)、D表示,画树状图如下:

由树状图知共有12种等可能结果,其中小明被选中的结果数为6,
∴小明被选中的概率为![]() =
=![]() .
.

【题目】某果园有![]() 棵橘子树,平均每一棵树结
棵橘子树,平均每一棵树结![]() 个橘子.根据经验估计,每多种
个橘子.根据经验估计,每多种![]() 棵树,平均每棵树就会少结
棵树,平均每棵树就会少结![]() 个橘子.设果园增种
个橘子.设果园增种![]() 棵橘子树,果园橘子总个数为
棵橘子树,果园橘子总个数为![]() 个.
个.
(1)根据题意,填写下表:
增种的橘子树(棵) |
|
|
|
| … |
|
平均每棵树结橘子数(个) |
|
(2)求果园里增种多少棵橘子树时,所结橘子总数最多,并求出此时橘子的总数.