题目内容
如图1,矩形ABCD的边BC在x轴的正半轴上,点E(m,1)是对角线BD的中点,点A、E在反比例函数y=
的图象上.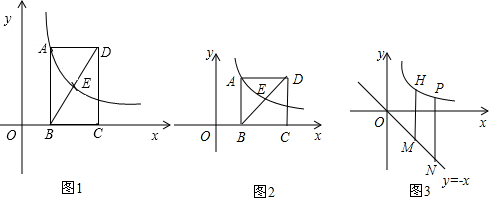
(1)求AB的长;
(2)当矩形ABCD是正方形时,将反比例函数y=
的图象沿y轴翻折,得到反比例函数y=
的图象(如图2),求k1的值;
(3)直线y=-x上有一长为
动线段MN,作MH、NP都平行y轴交在条件(2)下,第一象限内的双曲线y=
于点H、P,问四边形MHPN能否为平行四边形(如图3)?若能,请求出点M的坐标;若不能,请说明理由.
| k |
| x |

(1)求AB的长;
(2)当矩形ABCD是正方形时,将反比例函数y=
| k |
| x |
| k1 |
| x |
(3)直线y=-x上有一长为
| 2 |
| k |
| x |
分析:(1)过点E作EF⊥BC于F,可证EF为△BCD的中位线,根据三角形的中位线定理即可求出AB的长;
(2)当矩形ABCD是正方形时,由(1)知,BC=AB=2.先用含m的代数式表示点A的坐标,再根据点A、E在反比例函数y=
的图象上,列方程求出m的值,然后由轴对称的性质即可求出k1的值;
(3)过点N作NG⊥HM于G,易求MG=NG=1.设M(a,-a),则可用含a的代数式分别表示点N、P、H的坐标,由MH=NP列出关于a的方程,求解即可.
(2)当矩形ABCD是正方形时,由(1)知,BC=AB=2.先用含m的代数式表示点A的坐标,再根据点A、E在反比例函数y=
| k |
| x |
(3)过点N作NG⊥HM于G,易求MG=NG=1.设M(a,-a),则可用含a的代数式分别表示点N、P、H的坐标,由MH=NP列出关于a的方程,求解即可.
解答: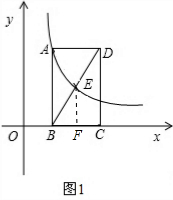 解:(1)如图,过点E作EF⊥BC于F,则EF=1.
解:(1)如图,过点E作EF⊥BC于F,则EF=1.
∵点E是对角线BD的中点,
∴F为BC的中点,EF为△BCD的中位线,
∴CD=2EF=2.
∵四边形ABCD是矩形,
∴AB=CD=2;
(2)由(1)知,AB=CD=2.
∵四边形ABCD是正方形,
∴BC=AB=2,∴BF=FC=1.
∵E(m,1),
∴F(m,0),B(m-1,0),A(m-1,2),
∵点A、E在反比例函数y=
的图象上,
∴k=2(m-1)=m×1,
解得m=2,k=2,
∴点A、E在反比例函数y=
的图象上.
∵将反比例函数y=
的图象沿y轴翻折,得到反比例函数y=
的图象,
∴k1=-2;
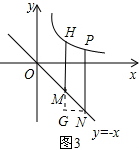 (3)四边形MHPN能为平行四边形.理由如下:
(3)四边形MHPN能为平行四边形.理由如下:
过点N作NG⊥HM于G,则∠MGN=90°.
∵点M、N在直线y=-x上,
∴∠MNG=45°,
∴MG=NG,
又∵MN=
,
∴MG=NG=1.
设M(a,-a),则N(a+1,-a-1).
∵MH、NP都平行y轴,且点H、P都在双曲线y=
的图象上,
∴H(a,
),P(a+1,
).
∵MH∥NP,
∴当MH=NP时,四边形MHPN为平行四边形,
此时
+a=
+a+1,
整理得a2+a-2=0,解得a=1,a=-2(舍去).
∴点M的坐标为(1,-1).
故四边形MHPN能为平行四边形,此时点M的坐标为(1,-1).
 解:(1)如图,过点E作EF⊥BC于F,则EF=1.
解:(1)如图,过点E作EF⊥BC于F,则EF=1.∵点E是对角线BD的中点,
∴F为BC的中点,EF为△BCD的中位线,
∴CD=2EF=2.
∵四边形ABCD是矩形,
∴AB=CD=2;
(2)由(1)知,AB=CD=2.
∵四边形ABCD是正方形,
∴BC=AB=2,∴BF=FC=1.
∵E(m,1),
∴F(m,0),B(m-1,0),A(m-1,2),
∵点A、E在反比例函数y=
| k |
| x |
∴k=2(m-1)=m×1,
解得m=2,k=2,
∴点A、E在反比例函数y=
| 2 |
| x |
∵将反比例函数y=
| 2 |
| x |
| k1 |
| x |
∴k1=-2;
 (3)四边形MHPN能为平行四边形.理由如下:
(3)四边形MHPN能为平行四边形.理由如下:过点N作NG⊥HM于G,则∠MGN=90°.
∵点M、N在直线y=-x上,
∴∠MNG=45°,
∴MG=NG,
又∵MN=
| 2 |
∴MG=NG=1.
设M(a,-a),则N(a+1,-a-1).
∵MH、NP都平行y轴,且点H、P都在双曲线y=
| 2 |
| x |
∴H(a,
| 2 |
| a |
| 2 |
| a+1 |
∵MH∥NP,
∴当MH=NP时,四边形MHPN为平行四边形,
此时
| 2 |
| a |
| 2 |
| a+1 |
整理得a2+a-2=0,解得a=1,a=-2(舍去).
∴点M的坐标为(1,-1).
故四边形MHPN能为平行四边形,此时点M的坐标为(1,-1).
点评:考查了反比例函数综合题,其中有三角形的中位线定理,矩形和正方形的性质,反比例函数和正比例函数,平行四边形的判定,解方程,有一定的难度.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
 如图,在矩形ABCD中,连接AC,如果O为△ABC的内心,过O作OE⊥AD于E,作OF⊥CD于F,则矩形OFDE的面积与矩形ABCD的面积的比值为( )
如图,在矩形ABCD中,连接AC,如果O为△ABC的内心,过O作OE⊥AD于E,作OF⊥CD于F,则矩形OFDE的面积与矩形ABCD的面积的比值为( )A、
| ||
B、
| ||
C、
| ||
| D、不能确定 |
 Q两点相遇时,它们同时停止运动.设P、Q两点运动的时间为x(秒),△APQ的面积为S(平方单位).
Q两点相遇时,它们同时停止运动.设P、Q两点运动的时间为x(秒),△APQ的面积为S(平方单位). (2013•广东模拟)如图,在矩形ABCD中,AC、BD交于点O,∠AEC=90°,连接OE,OF平分∠DOE交DE于F.
(2013•广东模拟)如图,在矩形ABCD中,AC、BD交于点O,∠AEC=90°,连接OE,OF平分∠DOE交DE于F. 如图,在矩形ABCD中,AB=3,BC=4,EF过AC、BD的交点O,则图中阴影部分的面积为
如图,在矩形ABCD中,AB=3,BC=4,EF过AC、BD的交点O,则图中阴影部分的面积为 (2013•南京)如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°),若∠1=110°,则∠α=
(2013•南京)如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°),若∠1=110°,则∠α=