题目内容
 (2013•广东模拟)如图,在矩形ABCD中,AC、BD交于点O,∠AEC=90°,连接OE,OF平分∠DOE交DE于F.
(2013•广东模拟)如图,在矩形ABCD中,AC、BD交于点O,∠AEC=90°,连接OE,OF平分∠DOE交DE于F.求证:OF垂直平分DE.
分析:根据矩形的对角线互相平分且相等可得OD=AO=CO=
AC,再根据直角三角形斜边上的中线等于斜边的一半可得OE=
AC,从而得到OE=OD,然后根据等腰三角形三线合一的性质证明即可.
| 1 |
| 2 |
| 1 |
| 2 |
解答:证明:在矩形ABCD中,OD=AO=CO=
AC,
∵∠AEC=90°,AO=CO,
∴OE=
AC,
∴OE=OD,
∵OF平分∠DOE,
∴OF垂直平分DE.
| 1 |
| 2 |
∵∠AEC=90°,AO=CO,
∴OE=
| 1 |
| 2 |
∴OE=OD,
∵OF平分∠DOE,
∴OF垂直平分DE.
点评:本题考查了矩形的对角线互相平分且相等的性质,直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形三线合一的性质,熟记性质是解题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
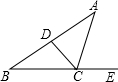 (2013•广东模拟)如右图,在△ABC中,DC是AB的垂直平分线,交AB于D,若∠B=41°,则外角∠ACE=
(2013•广东模拟)如右图,在△ABC中,DC是AB的垂直平分线,交AB于D,若∠B=41°,则外角∠ACE=