题目内容
【题目】将平行四边形纸片ABCD按如图方式折叠,使点C与点A重合,点D落到D’处,折痕为EF.
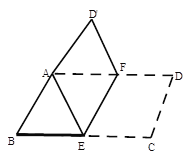
(1)、求证:△ABE≌△AD’F;
(2)、连接CF,判断四边形AECF是否为平行四边形?请证明你的结论。
(3)、若AE=5,求四边形AECF的周长。
【答案】(1)、证明过程见解析;(2)、平行四边形,证明过程见解析;(3)、20
【解析】试题分析:(1)、根据ABCD为平行四边形得出AB=CD,∠B=∠D,AD∥BC,根据折叠得出AB=AD′,根据AD∥BC得出∠BEA=∠EAD,根据D′F∥AE得出∠EAD=∠D′FA,从而说明∠BEA=∠D′FA,得出三角形全等;(2)、根据△ABE≌△AD′F 得出AE=AF,根据折叠得出AE=EC,从而说明AF=CE,根据ABCD′是平行四边形得出BC∥AD′,即AF∥BC,从而说明平行四边形;(3)、根据题意得出AE=EC=5,根据四边形AECF的周长=2(AE+EC)得出答案.
试题解析:(1)、∵四边形ABCD为平行四边形 ∴AB=CD,∠B=∠D,AD∥BC
又∵点C与点A重合,点D落在点D′处 ∴CD=AD′ 即AB=AD′ ∵AD∥BC ∴∠BEA=∠EAD
又∵D′F∥AE ∴∠EAD=∠D′FA ∴∠BEA=∠D′FA ∴△ABE≌△AD′F(AAS)
(2)、连接CF,四边形AECF为平行四边形
由(1)得:△ABE≌△AD′F ∴AE=AF 根据折叠可得:AE=EC ∴AF=EC
又∵四边形ABCD′是平行四边形 ∴BC∥AD′ ∴AF∥EC ∴四边形AECF为平行四边形
(3)、∵AE=EC AE=5 ∴四边形AECF的周长=2(AE+EC)=2×(5+5)=20.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目