题目内容
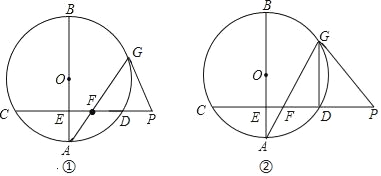
【题目】如图,⊙O中,AC为直径,MA,MB分别切⊙O于点A,B,∠BAC=25°,则∠AMB的大小为( )
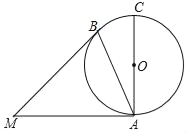
A. 25°B. 30°C. 45°D. 50°
【答案】D
【解析】
由AM与圆O相切,根据切线的性质得到AM垂直于AC,可得出∠MAC为直角,再由∠BAC的度数,用∠MAC﹣∠BAC求出∠MAB的度数,又MA,MB为圆O的切线,根据切线长定理得到MA=MB,利用等边对等角可得出∠MAB=∠MBA,由底角的度数,利用三角形的内角和定理即可求出∠AMB的度数.
解:∵MA切⊙O于点A,AC为直径,
∴∠MAC=90°,又∠BAC=25°,
∴∠MAB=∠MAC﹣∠BAC=65°,
∵MA、MB分别切⊙O于点A、B,
∴MA=MB,
∴∠MAB=∠MBA=65°,
∴∠AMB=180°﹣(∠MAB+∠MBA)=50°,
故选:D.

练习册系列答案
相关题目
【题目】每年5月20日是中国学生营养日,按时吃早餐是一种健廉的饮食习惯,为了解本校九年级学生饮食习惯,某兴趣小组在九年级随机抽查了一部分学生每天吃早餐的情况,并将统计结果绘制成如下不完
整的统计图表:
组别 | 调查结果 | 所占百分比 |
A | 不吃早餐 | 25% |
B | 偶尔吃早餐 | 12.5% |
C | 经常吃早餐 | |
D | 每天吃早餐 | 50% |

请根据以上统计图表,解答下列问题:
(1)本次接受调查的总人数为多少人.
(2)请补全条形统计图.
(3)该校九年级共有学生1200人,请估计该校九年级学生每天吃早餐的人数:
(4)请根据此次调查的结果提一条建议.