题目内容
【题目】如图,在四边形ABCD中,AB:BC:CD:DA=2:2:3:1,且∠ABC=90°,则∠DAB的度数是______°.
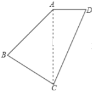
【答案】135°
【解析】
由已知可得AB=BC,从而可求得∠BAC的度数.设AB=2x ,通过计算证明AC2+AD2=CD2,从而证得ΔACD是直角三角形,即可得到∠DAC=90°,从而求得∠DAB的度数.
解:∵AB:BC:CD:DA=2:2:3:1,且∠ABC=90°,
∴AB=BC,
∴∠BAC=∠ACB=45°,
∴设AB=2x,则BC=2x,CD=3x,DA=x,
∴AC2=AB2+BC2=(2x)2+(2x)2=8x2
又CD2-AD2=(3x)2-x2=8x2
∴AC2= CD2-AD2
∵AC2+AD2=CD2
∴ΔACD是直角三角形,
∴∠DAC=90°,
∴∠DAB=45°+90°=135°.
故答案是:135°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】王明同学随机抽查某市![]() 个小区所得到的绿化率情况,结果如下表:
个小区所得到的绿化率情况,结果如下表:
小区绿化率 |
|
|
|
|
小区个数 |
|
|
|
|
则关于这![]() 个小区的绿化率情况,下列说法错误的是( )
个小区的绿化率情况,下列说法错误的是( )
A. 极差是13% B. 众数是25% C. 中位数是25% D. 平均数是26.2%