题目内容
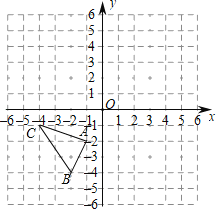
【题目】如图，平面直角坐标系中，△ABC的三个顶点的坐标分别为A（﹣1，﹣2），B（﹣2，﹣4），C（﹣4，﹣1）．
（1）在平面直角坐标系中画出与△ABC关于点P（1，0）成中心对称的△A'B'C'，并分别写出点A'，B'，C'的坐标；
（2）如果点M（a，b）是△ABC边上（不与A，B，C重合）任意一点，请写出在△A'B'C'上与点M对应的点M'的坐标．
【答案】（1）△A'B'C'见解析，A′（3，2），B′（4，4），C′（6，1）；（2）M′（2a，b）．
【解析】
（1）分别作出A，B，C的对应点A′、B′、C′，然后顺次连接可得△A'B'C'，再根据所作图形写出坐标即可．
（2）利用中点坐标公式计算即可．
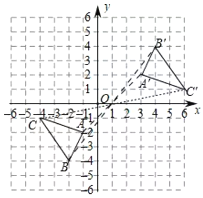
解：（1）△A'B'C'如图所示，A′（3，2），B′（4，4），C′（6，1）；
（2）设M′（m，n），
则有
，
，
∴m＝2a，n＝b，
∴M′（2a，b）．
练习册系列答案
相关题目
