题目内容
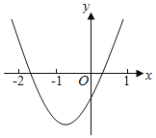
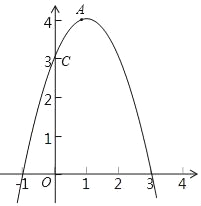
【题目】如图,已知二次函数y=ax2+2x+c图象经过点A (1,4)和点C (0,3).
(1)求该二次函数的解析式;
(2)结合函数图象,直接回答下列问题:
①当﹣1<x<2时,求函数y的取值范围: .
②当y≥3时,求x的取值范围: .
【答案】(1)y=﹣x2+2x+3;(2)0<y≤4,0≤x≤2.
【解析】
(1)把A点和C点坐标代入y=ax2+2x+c得到二元一次方程组,然后解方程组求出a、c即可得到抛物线解析式;
(2)①先分别计算出x为-1和2时的函数值,然后根据二次函数的性质写出对应的函数值的范围;②先计算出函数值为3所对应的自变量的值,然后根据二次函数的性质写出y≥3时,x的取值范围.
(1)将点A和点C的坐标代入函数解析式,得![]() ,
,
解得![]() ,
,
二次函数的解析式为y=﹣x2+2x+3;
(2)由图象知,①当﹣1<x<2时,求函数y的取值范围:0<y≤4.
②当y≥3时,求x的取值范围:0≤x≤2.
故答案为:0<y≤4,0≤x≤2.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
【题目】王明同学随机抽查某市![]() 个小区所得到的绿化率情况,结果如下表:
个小区所得到的绿化率情况,结果如下表:
小区绿化率 |
|
|
|
|
小区个数 |
|
|
|
|
则关于这![]() 个小区的绿化率情况,下列说法错误的是( )
个小区的绿化率情况,下列说法错误的是( )
A. 极差是13% B. 众数是25% C. 中位数是25% D. 平均数是26.2%