题目内容
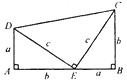
【题目】历史上对勾股定理的一种证法采用了如图所示图形，其中两个全等的直角三角形边AE，EB在一条直线上．证明中用到的面积相等关系是 ( )
A. S△EDA=S△CEB
B. S△EDA +S△CEB=S△CDB
C. S四边形CDAE= S四边形CDEB
D. S△EDA+S△CDE+S△CEB= S四边形ABCD
【答案】D
【解析】
用三角形的面积和、梯形的面积来表示这个图形的面积，从而证明勾股定理．
∵由S△EDA+S△CDE+S△CEB=S四边形ABCD．
可知
ab+c2+ab=（a+b）2，
∴c2+2ab=a2+2ab+b2，整理得a2+b2=c2，
∴证明中用到的面积相等关系是：S△EDA+S△CDE+S△CEB=S四边形ABCD．
故选D．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
