题目内容
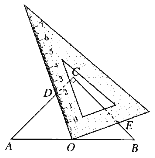
【题目】如图,在等腰直角△ABC中,∠C=90°,点O是AB的中点,边AC的长为![]() ,将一块边长足够大的三角板的直角顶点放在点O处,将三角板绕点O旋转,始终保持三角板的一条直角边与 AC相交,交点为点D,另一条直角边与BC相交,交点为点E.证明:等腰直角三角形ABC的边被三角板覆盖部分的两条线段CD与CE长度之和为定值
,将一块边长足够大的三角板的直角顶点放在点O处,将三角板绕点O旋转,始终保持三角板的一条直角边与 AC相交,交点为点D,另一条直角边与BC相交,交点为点E.证明:等腰直角三角形ABC的边被三角板覆盖部分的两条线段CD与CE长度之和为定值![]() .
.
【答案】见解析.
【解析】
连接OC,证明△OCD≌△OBE,根据全等三角形的性质得到CD=BE,证明结论.
连接OC.
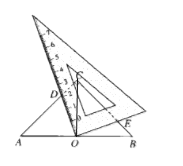
∵AC=BC,AO=BO,∠ACB=90°.
∴∠ACO=∠BCO=![]() ∠ACB=45°,OC⊥AB.
∠ACB=45°,OC⊥AB.
∠A=∠B=45°.
∴OC=OB.
∵∠BOE+∠EOD+∠AOD=180°,∠EOD=90°.
∴∠BOE+∠AOD=90°.
又∵∠COD+∠AOD=90°,
∴∠BOE=∠COD.
又∠OCD=∠B=45°,
∴△OCD≌△OBE.
∴CD=BE.
∴CD+CE=BE+CE=BC=![]() .
.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目