题目内容
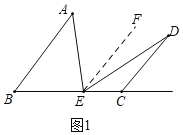
【题目】点D在∠ABC内,点E为边BC上一点,连接DE、CD.
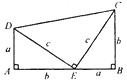
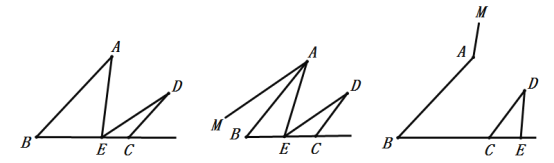
(1)如图1,连接AE,若∠AED=∠A+∠D,求证:AB//CD.
(2)在(1)的结论下,过点A的直线MA//ED.
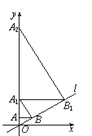
①如图2,当点E在线段BC上时,猜想并验证∠MAB与∠CDE的数量关系;
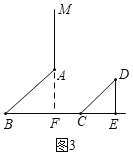
②如图3,当点E在线段BC的延长线上时,猜想并验证∠MAB与∠CDE的数量关系.
【答案】(1)证明见解析;(2)①∠MAB=∠CDE;②∠CDE+∠MAB=180°.
【解析】
(1)过E作EF∥AB,则∠A=∠AEF,由∠D=∠AED﹣∠A,∠DEF=∠AED﹣∠AEF,即可得到∠D=∠DEF,进而得出EF∥CD,即可得到AB∥CD;
(2)①根据∠AED=∠BAE+∠D,∠MAE=∠BAE+∠BAE,即可得到∠D=∠BAM,即可得到结论;
②延长MA交BC于F,依据平行线的性质以及三角形内角和定理,即可得到∠D=∠BAF,再根据邻补角互补即可得到∠CDE+∠MAB=180°.
(1)如图1,过E作EF∥AB,则∠A=∠AEF.
∵∠AED=∠A+∠D,∴∠D=∠AED﹣∠A.
又∵∠DEF=∠AED﹣∠AEF,∴∠D=∠DEF,∴EF∥CD,∴AB∥CD;
(2)①∵AM∥DE,∴∠MAE=∠AED.
∵∠AED=∠BAE+∠D,∠MAE=∠BAE+∠BAE,∴∠D=∠BAM,即∠MAB=∠CDE;
②如图3,延长MA交BC于F.
∵MA∥ED,∴∠DEC=∠MFB.
∵AB∥CD,∴∠B=∠DCE,∴∠D=∠BAF.
又∵∠BAF+∠MAB=180°,∴∠CDE+∠MAB=180°.

练习册系列答案
相关题目