Question

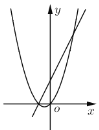
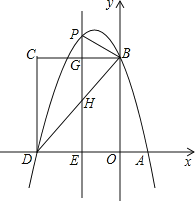
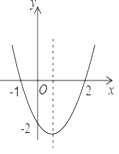
【题目】如图，二次函数y＝ax2+bx+c的图象如图所示，以下结论：①abc＞0； ②b2-4ac＜0 ； ③2a+b＞0 ；④a+b+c＞0，其中正确的个数（ ）

A.1B.2C.3D.4

Answer 1

【答案】B

【解析】

由抛物线开口向上，得到a大于0，再由对称轴在y轴右侧得到a与b异号，可得出b小于0，由抛物线与y轴交于负半轴，得到c小于0，可得出abc大于0，判断出选项①正确；由抛物线与x轴交于两点，得到根的判别式大于0；利用对称轴公式表示出对称轴，由图象得到对称轴小于1，再由a大于0，利用不等式的基本性质变形即可得到2a+b的正负；由图象可得出当x=1时对应二次函数图象上的点在x轴下方，即将x=1代入二次函数解析式，得到a+b+c的正负．

解：∵抛物线开口向上，对称轴在y轴右侧，且抛物线与y轴交于负半轴，
∴a＞0，b＜0，c＜0，
∴abc＞0，故选项①正确；
∵抛物线与x轴有两个交点，
∴b2-4ac＞0，故选项②错误；
∵由图象得：对称轴为直线x=＜1，且a＞0，
∴2a+b＞0，故选项③正确；
由图象可得：当x=1时，对应的函数图象上的点在x轴下方，
∴将x=1代入y＝ax2+bx+c得：y=a+b+c＜0，故选项④错误，

综上，正确的选项有：①③共2个．
故选：B．